Capacity Bounded Differential Privacy
Paper and Code
Jul 03, 2019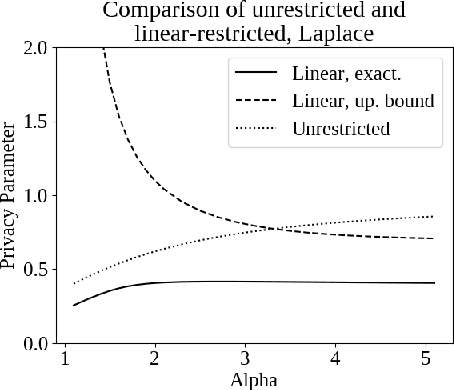
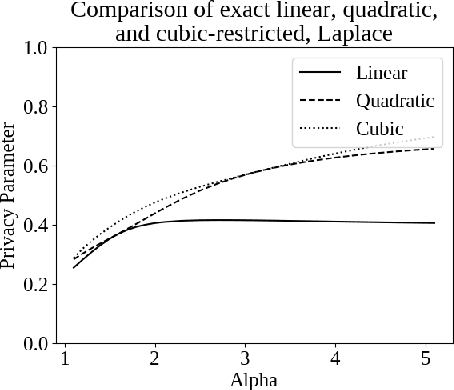
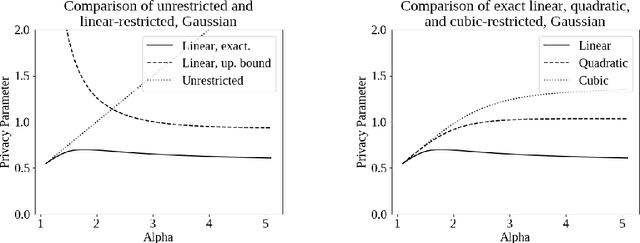
Differential privacy, a notion of algorithmic stability, is a gold standard for measuring the additional risk an algorithm's output poses to the privacy of a single record in the dataset. Differential privacy is defined as the distance between the output distribution of an algorithm on neighboring datasets that differ in one entry. In this work, we present a novel relaxation of differential privacy, capacity bounded differential privacy, where the adversary that distinguishes output distributions is assumed to be capacity-bounded -- i.e. bounded not in computational power, but in terms of the function class from which their attack algorithm is drawn. We model adversaries in terms of restricted f-divergences between probability distributions, and study properties of the definition and algorithms that satisfy them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge