A Quantum-inspired Hybrid Swarm Intelligence and Decision-Making for Multi-Criteria ADAS Calibration

The tuning of Advanced Driver Assistance Systems (ADAS) involves resolving trade-offs among several competing objectives, including operational safety, system responsiveness, energy usage, and passenger comfort. This work introduces a novel optimization framework based on Quantum-Inspired Hybrid Swarm Intelligence (QiHSI), in which quantum-inspired mechanisms are embedded within a multi-objective salp swarm optimization process to strengthen global search capability and preserve population diversity in complex, high-dimensional decision spaces. In addition, a decision-maker-in-the-loop strategy is incorporated to incorporate adaptive expert guidance, enabling the optimization process to respond dynamically to changing design priorities and system constraints. The effectiveness of QiHSI is assessed using established multi-objective benchmark problems as well as a practical ADAS calibration scenario. Experimental comparisons with several state-of-the-art evolutionary and swarm-based algorithms, including MSSA, MOPSO, MOEA/D, SPEA2, NSGA-III, and RVEA, show that the proposed method consistently produces well-distributed Pareto-optimal solutions with faster convergence and improved adaptability. These findings demonstrate that QiHSI offers a reliable and scalable approach for intelligent ADAS calibration, supporting the development of more responsive, efficient, and safety-oriented autonomous driving technologies.

Parts of Speech Tagging in NLP: Runtime Optimization with Quantum Formulation and ZX Calculus

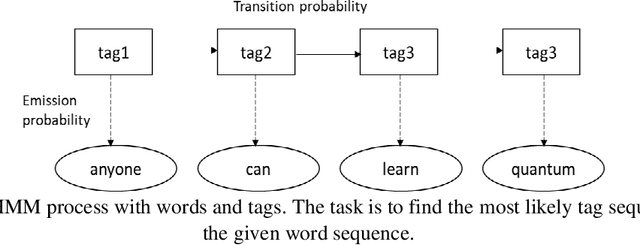
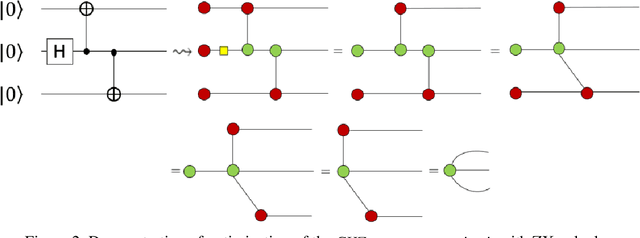
This paper proposes an optimized formulation of the parts of speech tagging in Natural Language Processing with a quantum computing approach and further demonstrates the quantum gate-level runnable optimization with ZX-calculus, keeping the implementation target in the context of Noisy Intermediate Scale Quantum Systems (NISQ). Our quantum formulation exhibits quadratic speed up over the classical counterpart and further demonstrates the implementable optimization with the help of ZX calculus postulates.

An Investigation of Quantum Deep Clustering Framework with Quantum Deep SVM & Convolutional Neural Network Feature Extractor

In this paper, we have proposed a deep quantum SVM formulation, and further demonstrated a quantum-clustering framework based on the quantum deep SVM formulation, deep convolutional neural networks, and quantum K-Means clustering. We have investigated the run time computational complexity of the proposed quantum deep clustering framework and compared with the possible classical implementation. Our investigation shows that the proposed quantum version of deep clustering formulation demonstrates a significant performance gain (exponential speed up gains in many sections) against the possible classical implementation. The proposed theoretical quantum deep clustering framework is also interesting & novel research towards the quantum-classical machine learning formulation to articulate the maximum performance.

An All-Pair Quantum SVM Approach for Big Data Multiclass Classification

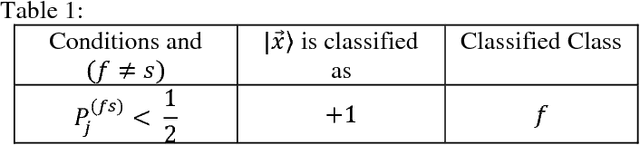
In this paper, we have discussed a quantum approach for the all-pair multiclass classification problem. We have shown that the multiclass support vector machine for big data classification with a quantum all-pair approach can be implemented in logarithm runtime complexity on a quantum computer. In an all-pair approach, there is one binary classification problem for each pair of classes, and so there are k (k-1)/2 classifiers for a k-class problem. As compared to the classical multiclass support vector machine that can be implemented with polynomial run time complexity, our approach exhibits exponential speed up in the quantum version. The quantum all-pair algorithm can be used with other classification algorithms, and a speed up gain can be achieved as compared to their classical counterparts.

Big Data Quantum Support Vector Clustering

Clustering is a complex process in finding the relevant hidden patterns in unlabeled datasets, broadly known as unsupervised learning. Support vector clustering algorithm is a well-known clustering algorithm based on support vector machines and Gaussian kernels. In this paper, we have investigated the support vector clustering algorithm in quantum paradigm. We have developed a quantum algorithm which is based on quantum support vector machine and the quantum kernel (Gaussian kernel and polynomial kernel) formulation. The investigation exhibits approximately exponential speed up in the quantum version with respect to the classical counterpart.

Gaussian Kernel in Quantum Paradigm

Gaussian kernel is a very popular kernel function used in many machine learning algorithms, especially in support vector machines (SVM). For nonlinear training instances in machine learning, it often outperforms polynomial kernels in model accuracy. The Gaussian kernel is heavily used in formulating nonlinear classical SVM. A very elegant quantum version of least square support vector machine which is exponentially faster than the classical counterparts was discussed in literature with quantum polynomial kernel. In this paper, we have demonstrated a quantum version of the Gaussian kernel and analyzed its complexity, which is O(\epsilon^(-1)logN) with N-dimensional instances and an accuracy \epsilon. The Gaussian kernel is not only more efficient than polynomial kernel but also has broader application range than polynomial kernel.

Solving Combinatorial Optimization problems with Quantum inspired Evolutionary Algorithm Tuned using a Novel Heuristic Method

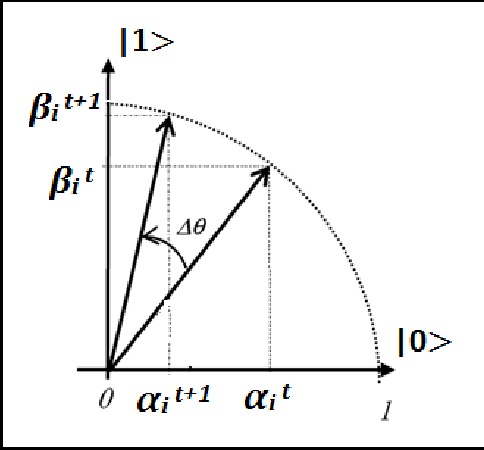
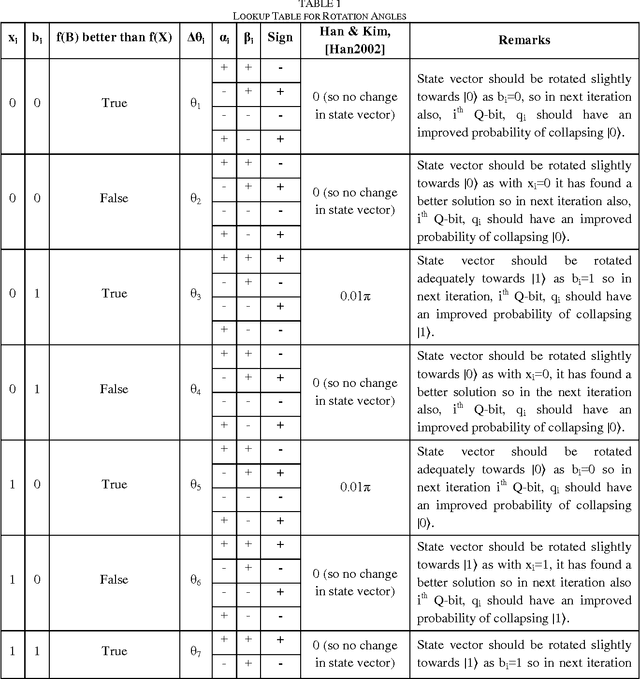
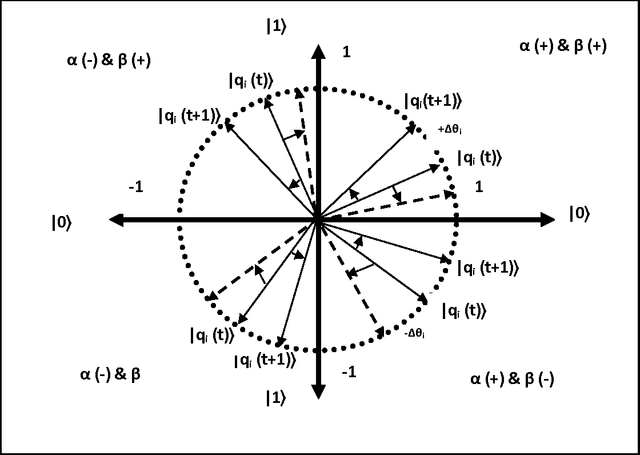
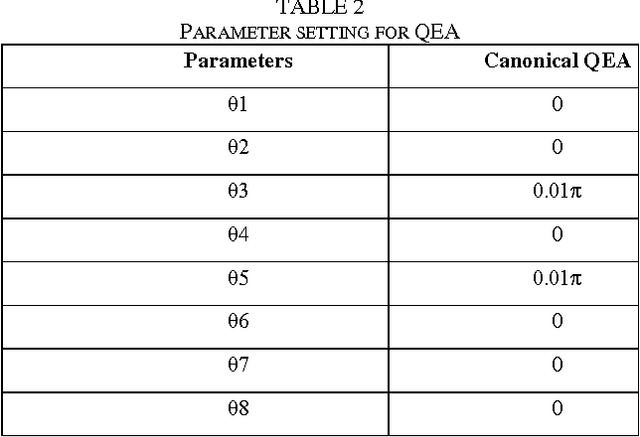
Quantum inspired Evolutionary Algorithms were proposed more than a decade ago and have been employed for solving a wide range of difficult search and optimization problems. A number of changes have been proposed to improve performance of canonical QEA. However, canonical QEA is one of the few evolutionary algorithms, which uses a search operator with relatively large number of parameters. It is well known that performance of evolutionary algorithms is dependent on specific value of parameters for a given problem. The advantage of having large number of parameters in an operator is that the search process can be made more powerful even with a single operator without requiring a combination of other operators for exploration and exploitation. However, the tuning of operators with large number of parameters is complex and computationally expensive. This paper proposes a novel heuristic method for tuning parameters of canonical QEA. The tuned QEA outperforms canonical QEA on a class of discrete combinatorial optimization problems which, validates the design of the proposed parameter tuning framework. The proposed framework can be used for tuning other algorithms with both large and small number of tunable parameters.