Comprehensive Study on Performance Evaluation and Optimization of Model Compression: Bridging Traditional Deep Learning and Large Language Models

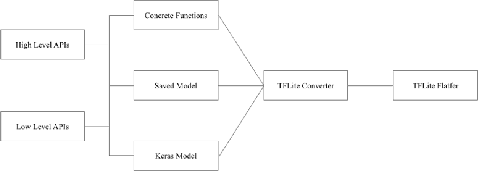
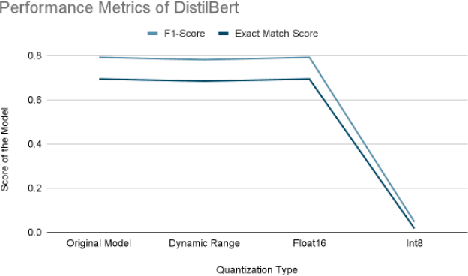
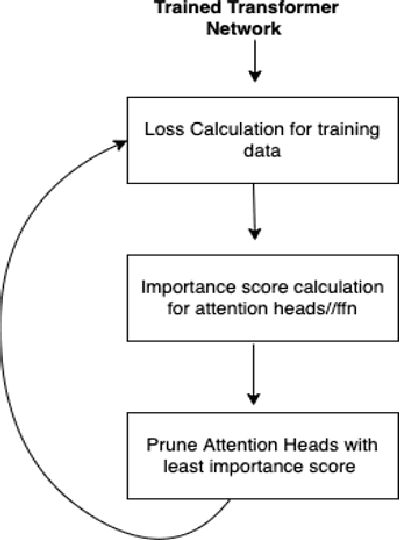
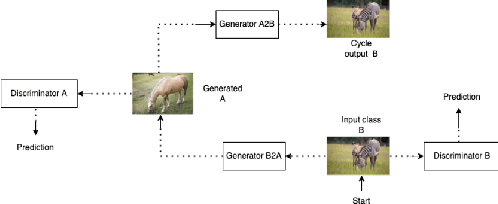
Deep learning models have achieved tremendous success in most of the industries in recent years. The evolution of these models has also led to an increase in the model size and energy requirement, making it difficult to deploy in production on low compute devices. An increase in the number of connected devices around the world warrants compressed models that can be easily deployed at the local devices with low compute capacity and power accessibility. A wide range of solutions have been proposed by different researchers to reduce the size and complexity of such models, prominent among them are, Weight Quantization, Parameter Pruning, Network Pruning, low-rank representation, weights sharing, neural architecture search, knowledge distillation etc. In this research work, we investigate the performance impacts on various trained deep learning models, compressed using quantization and pruning techniques. We implemented both, quantization and pruning, compression techniques on popular deep learning models used in the image classification, object detection, language models and generative models-based problem statements. We also explored performance of various large language models (LLMs) after quantization and low rank adaptation. We used the standard evaluation metrics (model's size, accuracy, and inference time) for all the related problem statements and concluded this paper by discussing the challenges and future work.

Investigation into the Potential of Parallel Quantum Annealing for Simultaneous Optimization of Multiple Problems: A Comprehensive Study

Parallel Quantum Annealing is a technique to solve multiple optimization problems simultaneously. Parallel quantum annealing aims to optimize the utilization of available qubits on a quantum topology by addressing multiple independent problems in a single annealing cycle. This study provides insights into the potential and the limitations of this parallelization method. The experiments consisting of two different problems are integrated, and various problem dimensions are explored including normalization techniques using specific methods such as DWaveSampler with Default Embedding, DWaveSampler with Custom Embedding and LeapHybridSampler. This method minimizes idle qubits and holds promise for substantial speed-up, as indicated by the Time-to-Solution (TTS) metric, compared to traditional quantum annealing, which solves problems sequentially and may leave qubits unutilized.

Parts of Speech Tagging in NLP: Runtime Optimization with Quantum Formulation and ZX Calculus

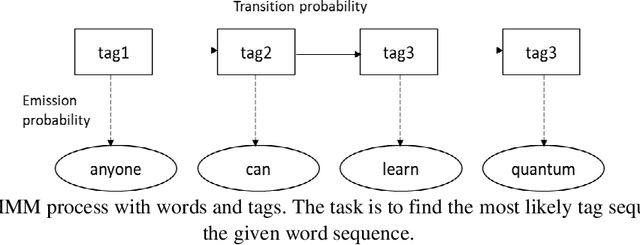
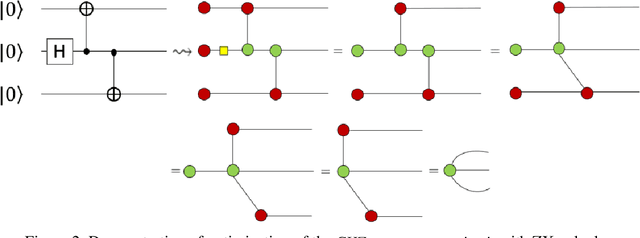
This paper proposes an optimized formulation of the parts of speech tagging in Natural Language Processing with a quantum computing approach and further demonstrates the quantum gate-level runnable optimization with ZX-calculus, keeping the implementation target in the context of Noisy Intermediate Scale Quantum Systems (NISQ). Our quantum formulation exhibits quadratic speed up over the classical counterpart and further demonstrates the implementable optimization with the help of ZX calculus postulates.

An Investigation of Quantum Deep Clustering Framework with Quantum Deep SVM & Convolutional Neural Network Feature Extractor

In this paper, we have proposed a deep quantum SVM formulation, and further demonstrated a quantum-clustering framework based on the quantum deep SVM formulation, deep convolutional neural networks, and quantum K-Means clustering. We have investigated the run time computational complexity of the proposed quantum deep clustering framework and compared with the possible classical implementation. Our investigation shows that the proposed quantum version of deep clustering formulation demonstrates a significant performance gain (exponential speed up gains in many sections) against the possible classical implementation. The proposed theoretical quantum deep clustering framework is also interesting & novel research towards the quantum-classical machine learning formulation to articulate the maximum performance.

An All-Pair Quantum SVM Approach for Big Data Multiclass Classification

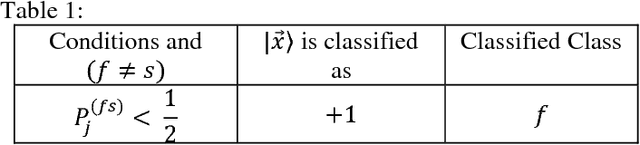
In this paper, we have discussed a quantum approach for the all-pair multiclass classification problem. We have shown that the multiclass support vector machine for big data classification with a quantum all-pair approach can be implemented in logarithm runtime complexity on a quantum computer. In an all-pair approach, there is one binary classification problem for each pair of classes, and so there are k (k-1)/2 classifiers for a k-class problem. As compared to the classical multiclass support vector machine that can be implemented with polynomial run time complexity, our approach exhibits exponential speed up in the quantum version. The quantum all-pair algorithm can be used with other classification algorithms, and a speed up gain can be achieved as compared to their classical counterparts.

Big Data Quantum Support Vector Clustering

Clustering is a complex process in finding the relevant hidden patterns in unlabeled datasets, broadly known as unsupervised learning. Support vector clustering algorithm is a well-known clustering algorithm based on support vector machines and Gaussian kernels. In this paper, we have investigated the support vector clustering algorithm in quantum paradigm. We have developed a quantum algorithm which is based on quantum support vector machine and the quantum kernel (Gaussian kernel and polynomial kernel) formulation. The investigation exhibits approximately exponential speed up in the quantum version with respect to the classical counterpart.

Gaussian Kernel in Quantum Paradigm

Gaussian kernel is a very popular kernel function used in many machine learning algorithms, especially in support vector machines (SVM). For nonlinear training instances in machine learning, it often outperforms polynomial kernels in model accuracy. The Gaussian kernel is heavily used in formulating nonlinear classical SVM. A very elegant quantum version of least square support vector machine which is exponentially faster than the classical counterparts was discussed in literature with quantum polynomial kernel. In this paper, we have demonstrated a quantum version of the Gaussian kernel and analyzed its complexity, which is O(\epsilon^(-1)logN) with N-dimensional instances and an accuracy \epsilon. The Gaussian kernel is not only more efficient than polynomial kernel but also has broader application range than polynomial kernel.