Dynamic Obstacle Avoidance with Bounded Rationality Adversarial Reinforcement Learning

Reinforcement Learning (RL) has proven largely effective in obtaining stable locomotion gaits for legged robots. However, designing control algorithms which can robustly navigate unseen environments with obstacles remains an ongoing problem within quadruped locomotion. To tackle this, it is convenient to solve navigation tasks by means of a hierarchical approach with a low-level locomotion policy and a high-level navigation policy. Crucially, the high-level policy needs to be robust to dynamic obstacles along the path of the agent. In this work, we propose a novel way to endow navigation policies with robustness by a training process that models obstacles as adversarial agents, following the adversarial RL paradigm. Importantly, to improve the reliability of the training process, we bound the rationality of the adversarial agent resorting to quantal response equilibria, and place a curriculum over its rationality. We called this method Hierarchical policies via Quantal response Adversarial Reinforcement Learning (Hi-QARL). We demonstrate the robustness of our method by benchmarking it in unseen randomized mazes with multiple obstacles. To prove its applicability in real scenarios, our method is applied on a Unitree GO1 robot in simulation.

Deep Learning Agents Trained For Avoidance Behave Like Hawks And Doves

We present heuristically optimal strategies expressed by deep learning agents playing a simple avoidance game. We analyse the learning and behaviour of two agents within a symmetrical grid world that must cross paths to reach a target destination without crashing into each other or straying off of the grid world in the wrong direction. The agent policy is determined by one neural network that is employed in both agents. Our findings indicate that the fully trained network exhibits behaviour similar to that of the game Hawks and Doves, in that one agent employs an aggressive strategy to reach the target while the other learns how to avoid the aggressive agent.

Robust Adversarial Reinforcement Learning via Bounded Rationality Curricula

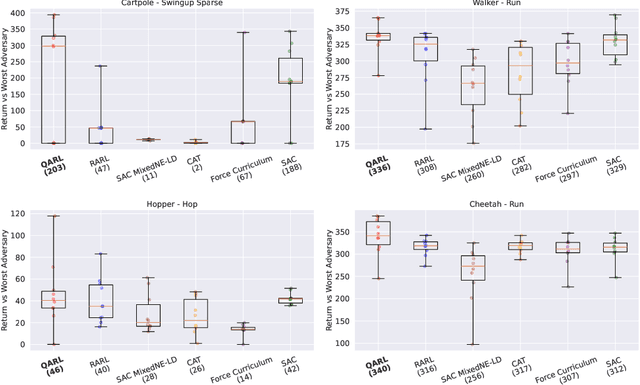
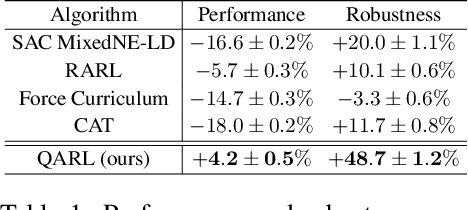
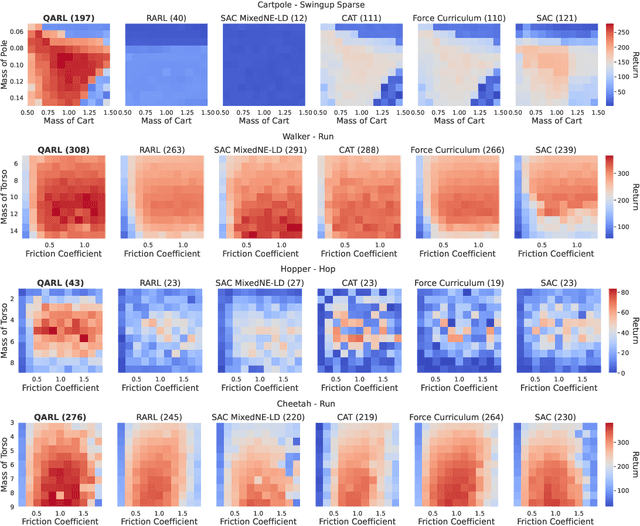
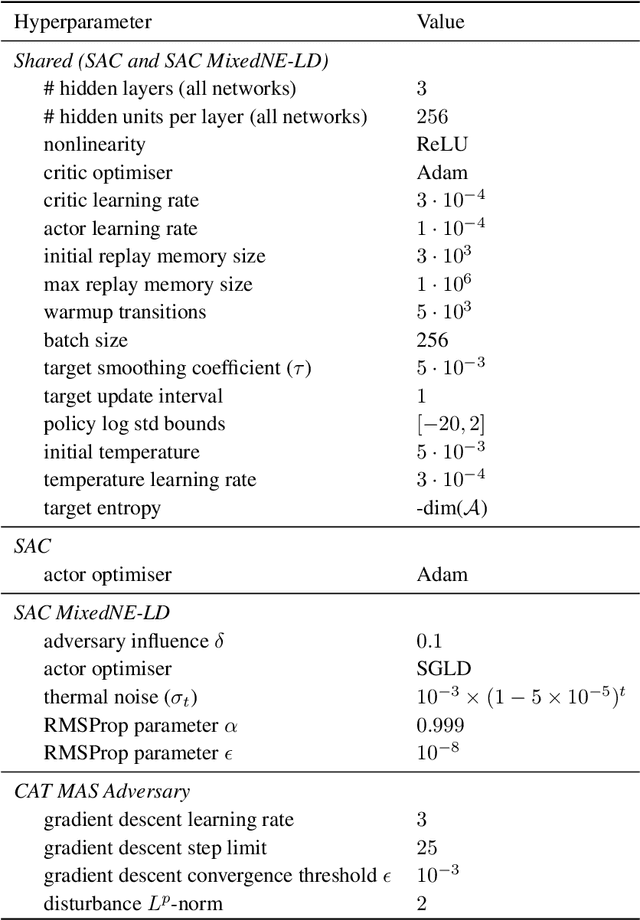
Robustness against adversarial attacks and distribution shifts is a long-standing goal of Reinforcement Learning (RL). To this end, Robust Adversarial Reinforcement Learning (RARL) trains a protagonist against destabilizing forces exercised by an adversary in a competitive zero-sum Markov game, whose optimal solution, i.e., rational strategy, corresponds to a Nash equilibrium. However, finding Nash equilibria requires facing complex saddle point optimization problems, which can be prohibitive to solve, especially for high-dimensional control. In this paper, we propose a novel approach for adversarial RL based on entropy regularization to ease the complexity of the saddle point optimization problem. We show that the solution of this entropy-regularized problem corresponds to a Quantal Response Equilibrium (QRE), a generalization of Nash equilibria that accounts for bounded rationality, i.e., agents sometimes play random actions instead of optimal ones. Crucially, the connection between the entropy-regularized objective and QRE enables free modulation of the rationality of the agents by simply tuning the temperature coefficient. We leverage this insight to propose our novel algorithm, Quantal Adversarial RL (QARL), which gradually increases the rationality of the adversary in a curriculum fashion until it is fully rational, easing the complexity of the optimization problem while retaining robustness. We provide extensive evidence of QARL outperforming RARL and recent baselines across several MuJoCo locomotion and navigation problems in overall performance and robustness.