On The Application of Linear Attention in Multimodal Transformers

Multimodal Transformers serve as the backbone for state-of-the-art vision-language models, yet their quadratic attention complexity remains a critical barrier to scalability. In this work, we investigate the viability of Linear Attention (LA) as a high-efficiency alternative within multimodal frameworks. By integrating LA, we reduce the computational overhead from quadratic to linear relative to sequence length while preserving competitive performance. We evaluate our approach across ViT-S/16, ViT-B/16, and ViT-L/16 architectures trained on the LAION-400M dataset, with validation focused on ImageNet-21K zero-shot accuracy. Our systematic evaluation demonstrates that Linear Attention not only yields significant computational savings but also adheres to the same scaling laws as standard softmax attention. These findings position Linear Attention as a robust, scalable solution for next-generation multimodal Transformers tasked with processing increasingly large and complex datasets.

FAST: Factorizable Attention for Speeding up Transformers

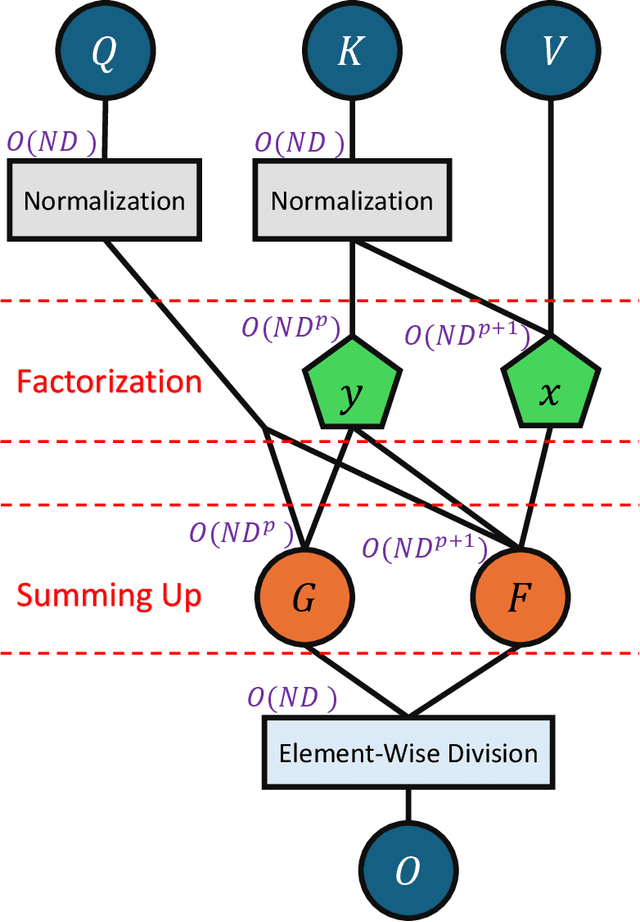
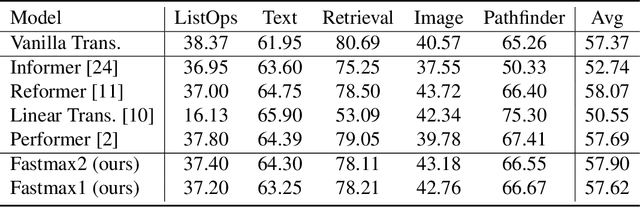
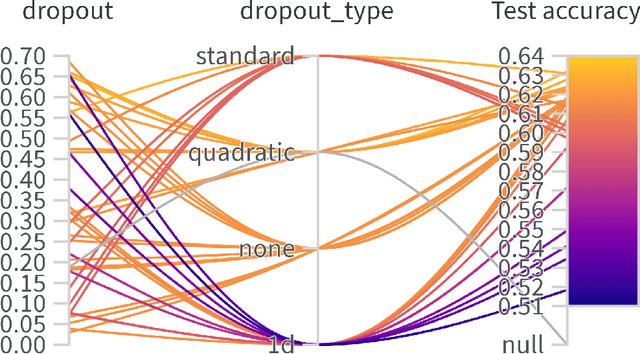
Motivated by the factorization inherent in the original fast multipole method and the improved fast Gauss transform we introduce a factorable form of attention that operates efficiently in high dimensions. This approach reduces the computational and memory complexity of the attention mechanism in transformers from $O(N^2)$ to $O(N)$. In comparison to previous attempts, our work presents a linearly scaled attention mechanism that maintains the full representation of the attention matrix without compromising on sparsification and incorporates the all-to-all relationship between tokens. We explore the properties of our new attention metric and conduct tests in various standard settings. Results indicate that our attention mechanism has a robust performance and holds significant promise for diverse applications where self-attention is used.