A Semi-Lagrangian Approach for Time and Energy Path Planning Optimization in Static Flow Fields

Efficient path planning for autonomous mobile robots is a critical problem across numerous domains, where optimizing both time and energy consumption is paramount. This paper introduces a novel methodology that considers the dynamic influence of an environmental flow field and considers geometric constraints, including obstacles and forbidden zones, enriching the complexity of the planning problem. We formulate it as a multi-objective optimal control problem, propose a novel transformation called Harmonic Transformation, and apply a semi-Lagrangian scheme to solve it. The set of Pareto efficient solutions is obtained considering two distinct approaches: a deterministic method and an evolutionary-based one, both of which are designed to make use of the proposed Harmonic Transformation. Through an extensive analysis of these approaches, we demonstrate their efficacy in finding optimized paths.

On the Generalization of Deep Reinforcement Learning Methods in the Problem of Local Navigation

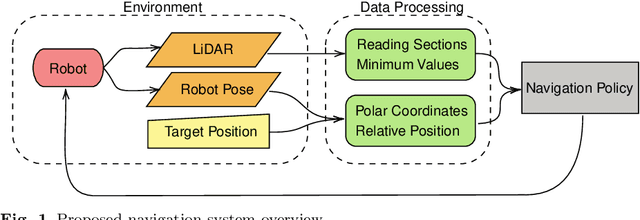
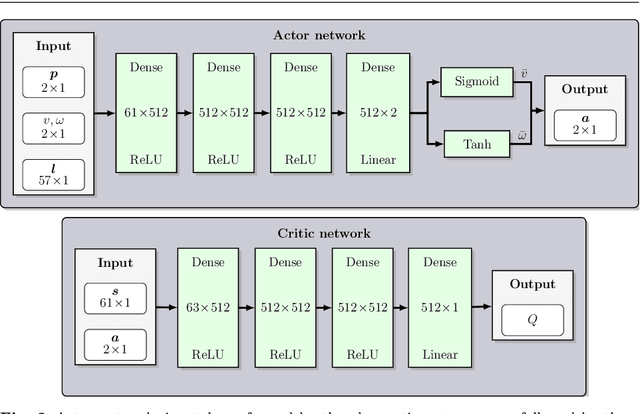
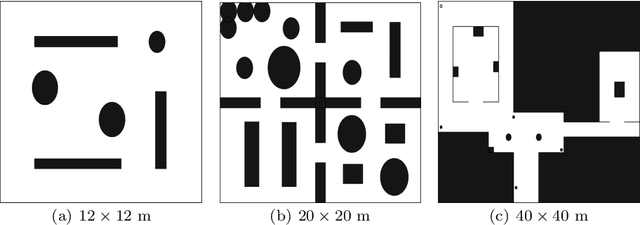
In this paper, we study the application of DRL algorithms in the context of local navigation problems, in which a robot moves towards a goal location in unknown and cluttered workspaces equipped only with limited-range exteroceptive sensors, such as LiDAR. Collision avoidance policies based on DRL present some advantages, but they are quite susceptible to local minima, once their capacity to learn suitable actions is limited to the sensor range. Since most robots perform tasks in unstructured environments, it is of great interest to seek generalized local navigation policies capable of avoiding local minima, especially in untrained scenarios. To do so, we propose a novel reward function that incorporates map information gained in the training stage, increasing the agent's capacity to deliberate about the best course of action. Also, we use the SAC algorithm for training our ANN, which shows to be more effective than others in the state-of-the-art literature. A set of sim-to-sim and sim-to-real experiments illustrate that our proposed reward combined with the SAC outperforms the compared methods in terms of local minima and collision avoidance.