Generalized Criterion for Identifiability of Additive Noise Models Using Majorization

The discovery of causal relationships from observational data is very challenging. Many recent approaches rely on complexity or uncertainty concepts to impose constraints on probability distributions, aiming to identify specific classes of directed acyclic graph (DAG) models. In this paper, we introduce a novel identifiability criterion for DAGs that places constraints on the conditional variances of additive noise models. We demonstrate that this criterion extends and generalizes existing identifiability criteria in the literature that employ (conditional) variances as measures of uncertainty in (conditional) distributions. For linear Structural Equation Models, we present a new algorithm that leverages the concept of weak majorization applied to the diagonal elements of the Cholesky factor of the covariance matrix to learn a topological ordering of variables. Through extensive simulations and the analysis of bank connectivity data, we provide evidence of the effectiveness of our approach in successfully recovering DAGs. The code for reproducing the results in this paper is available in Supplementary Materials.

An Alternative Graphical Lasso Algorithm for Precision Matrices

The Graphical Lasso (GLasso) algorithm is fast and widely used for estimating sparse precision matrices (Friedman et al., 2008). Its central role in the literature of high-dimensional covariance estimation rivals that of Lasso regression for sparse estimation of the mean vector. Some mysteries regarding its optimization target, convergence, positive-definiteness and performance have been unearthed, resolved and presented in Mazumder and Hastie (2011), leading to a new/improved (dual-primal) DP-GLasso. Using a new and slightly different reparametriztion of the last column of a precision matrix we show that the regularized normal log-likelihood naturally decouples into a sum of two easy to minimize convex functions one of which is a Lasso regression problem. This decomposition is the key in developing a transparent, simple iterative block coordinate descent algorithm for computing the GLasso updates with performance comparable to DP-GLasso. In particular, our algorithm has the precision matrix as its optimization target right at the outset, and retains all the favorable properties of the DP-GLasso algorithm.

Learning Bayesian Networks through Birkhoff Polytope: A Relaxation Method

We establish a novel framework for learning a directed acyclic graph (DAG) when data are generated from a Gaussian, linear structural equation model. It consists of two parts: (1) introduce a permutation matrix as a new parameter within a regularized Gaussian log-likelihood to represent variable ordering; and (2) given the ordering, estimate the DAG structure through sparse Cholesky factor of the inverse covariance matrix. For permutation matrix estimation, we propose a relaxation technique that avoids the NP-hard combinatorial problem of order estimation. Given an ordering, a sparse Cholesky factor is estimated using a cyclic coordinatewise descent algorithm which decouples row-wise. Our framework recovers DAGs without the need for an expensive verification of the acyclicity constraint or enumeration of possible parent sets. We establish numerical convergence of the algorithm, and consistency of the Cholesky factor estimator when the order of variables is known. Through several simulated and macro-economic datasets, we study the scope and performance of the proposed methodology.

Fused-Lasso Regularized Cholesky Factors of Large Nonstationary Covariance Matrices of Longitudinal Data

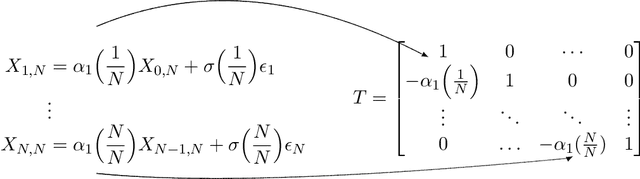
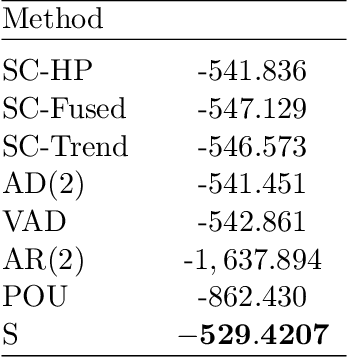
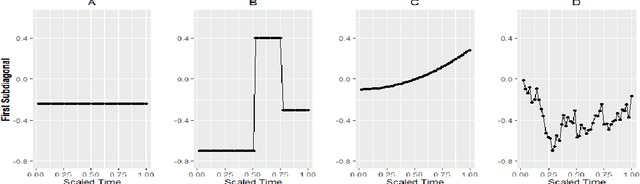
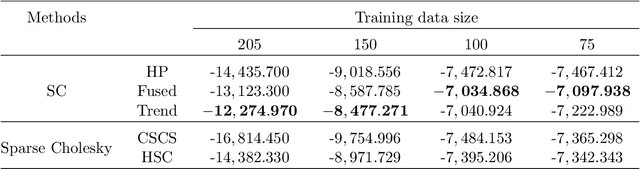
Smoothness of the subdiagonals of the Cholesky factor of large covariance matrices is closely related to the degrees of nonstationarity of autoregressive models for time series and longitudinal data. Heuristically, one expects for a nearly stationary covariance matrix the entries in each subdiagonal of the Cholesky factor of its inverse to be nearly the same in the sense that sum of absolute values of successive terms is small. Statistically such smoothness is achieved by regularizing each subdiagonal using fused-type lasso penalties. We rely on the standard Cholesky factor as the new parameters within a regularized normal likelihood setup which guarantees: (1) joint convexity of the likelihood function, (2) strict convexity of the likelihood function restricted to each subdiagonal even when $n<p$, and (3) positive-definiteness of the estimated covariance matrix. A block coordinate descent algorithm, where each block is a subdiagonal, is proposed and its convergence is established under mild conditions. Lack of decoupling of the penalized likelihood function into a sum of functions involving individual subdiagonals gives rise to some computational challenges and advantages relative to two recent algorithms for sparse estimation of the Cholesky factor which decouple row-wise. Simulation results and real data analysis show the scope and good performance of the proposed methodology.