Fused-Lasso Regularized Cholesky Factors of Large Nonstationary Covariance Matrices of Longitudinal Data

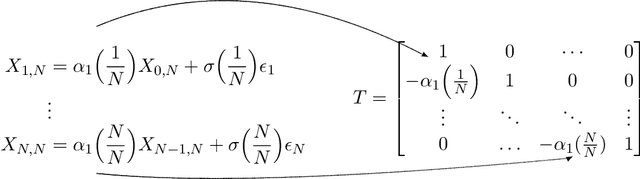
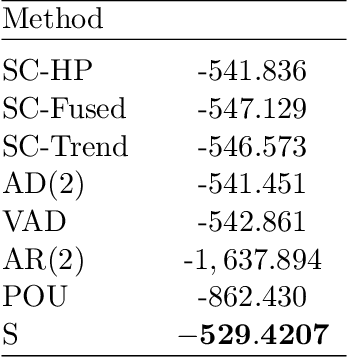
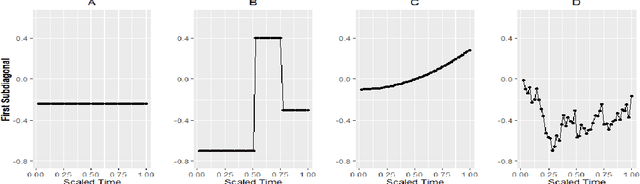
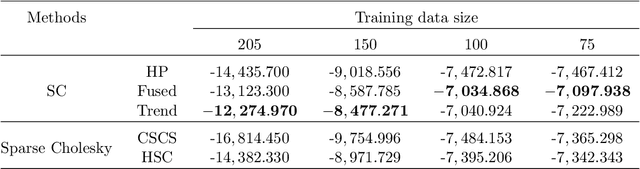
Smoothness of the subdiagonals of the Cholesky factor of large covariance matrices is closely related to the degrees of nonstationarity of autoregressive models for time series and longitudinal data. Heuristically, one expects for a nearly stationary covariance matrix the entries in each subdiagonal of the Cholesky factor of its inverse to be nearly the same in the sense that sum of absolute values of successive terms is small. Statistically such smoothness is achieved by regularizing each subdiagonal using fused-type lasso penalties. We rely on the standard Cholesky factor as the new parameters within a regularized normal likelihood setup which guarantees: (1) joint convexity of the likelihood function, (2) strict convexity of the likelihood function restricted to each subdiagonal even when $n<p$, and (3) positive-definiteness of the estimated covariance matrix. A block coordinate descent algorithm, where each block is a subdiagonal, is proposed and its convergence is established under mild conditions. Lack of decoupling of the penalized likelihood function into a sum of functions involving individual subdiagonals gives rise to some computational challenges and advantages relative to two recent algorithms for sparse estimation of the Cholesky factor which decouple row-wise. Simulation results and real data analysis show the scope and good performance of the proposed methodology.