Snail Homing and Mating Search Algorithm: A Novel Bio-Inspired Metaheuristic Algorithm

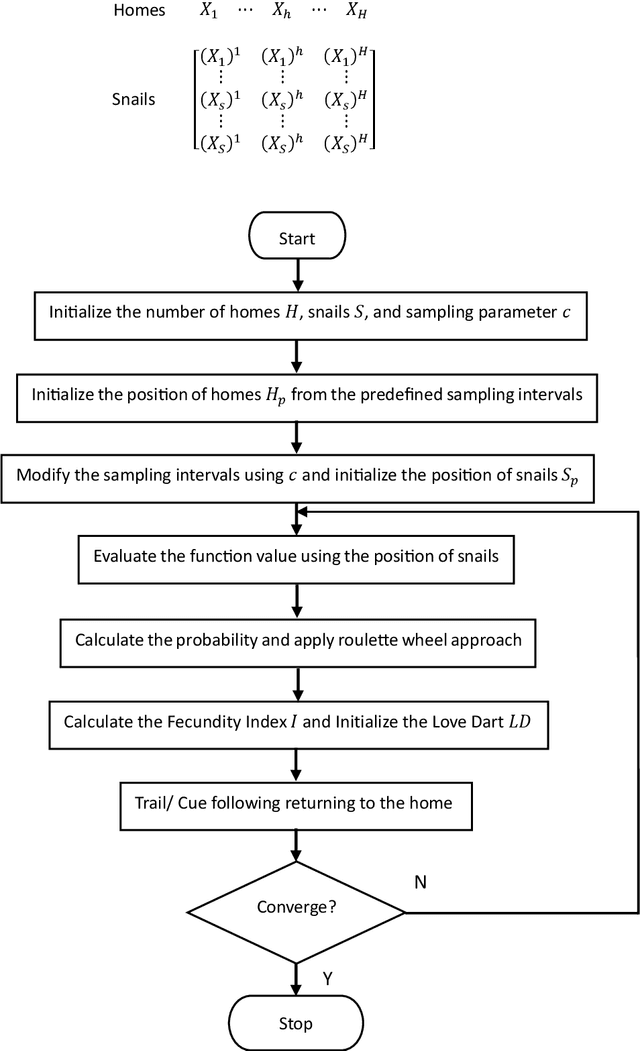
In this paper, a novel Snail Homing and Mating Search (SHMS) algorithm is proposed. It is inspired from the biological behaviour of the snails. Snails continuously travels to find food and a mate, leaving behind a trail of mucus that serves as a guide for their return. Snails tend to navigate by following the available trails on the ground and responding to cues from nearby shelter homes. The proposed SHMS algorithm is investigated by solving several unimodal and multimodal functions. The solutions are validated using standard statistical tests such as two-sided and pairwise signed rank Wilcoxon test and Friedman rank test. The solution obtained from the SHMS algorithm exhibited superior robustness as well as search space exploration capabilities within the less computational cost. The real-world application of SHMS algorithm is successfully demonstrated in the engineering design domain by solving three cases of design and economic optimization shell and tube heat exchanger problem. The objective function value and other statistical results obtained using SHMS algorithm are compared with other well-known metaheuristic algorithms.

Modified LAB Algorithm with Clustering-based Search Space Reduction Method for solving Engineering Design Problems

A modified LAB algorithm is introduced in this paper. It builds upon the original LAB algorithm (Reddy et al. 2023), which is a socio-inspired algorithm that models competitive and learning behaviours within a group, establishing hierarchical roles. The proposed algorithm incorporates the roulette wheel approach and a reduction factor introducing inter-group competition and iteratively narrowing down the sample space. The algorithm is validated by solving the benchmark test problems from CEC 2005 and CEC 2017. The solutions are validated using standard statistical tests such as two-sided and pairwise signed rank Wilcoxon test and Friedman rank test. The algorithm exhibited improved and superior robustness as well as search space exploration capabilities. Furthermore, a Clustering-Based Search Space Reduction (C-SSR) method is proposed, making the algorithm capable to solve constrained problems. The C-SSR method enables the algorithm to identify clusters of feasible regions, satisfying the constraints and contributing to achieve the optimal solution. This method demonstrates its effectiveness as a potential alternative to traditional constraint handling techniques. The results obtained using the Modified LAB algorithm are then compared with those achieved by other recent metaheuristic algorithms.