Fig Tree-Wasp Symbiotic Coevolutionary Optimization Algorithm

The nature inspired algorithms are becoming popular due to their simplicity and wider applicability. In the recent past several such algorithms have been developed. They are mainly bio-inspired, swarm based, physics based and socio-inspired; however, the domain based on symbiotic relation between creatures is still to be explored. A novel metaheuristic optimization algorithm referred to as Fig Tree-Wasp Symbiotic Coevolutionary (FWSC) algorithm is proposed. It models the symbiotic coevolutionary relationship between fig trees and wasps. More specifically, the mating of wasps, pollinating the figs, searching for new trees for pollination and wind effect drifting of wasps are modeled in the algorithm. These phenomena help in balancing the two important aspects of exploring the search space efficiently as well as exploit the promising regions. The algorithm is successfully tested on a variety of test problems. The results are compared with existing methods and algorithms. The Wilcoxon Signed Rank Test and Friedman Test are applied for the statistical validation of the algorithm performance. The algorithm is also further applied to solve the real-world engineering problems. The performance of the FWSC underscored that the algorithm can be applied to wider variety of real-world problems.

Solution to Advanced Manufacturing Process Problems using Cohort Intelligence Algorithm with Improved Constraint Handling Approaches

Recently, various Artificial Intelligence (AI) based optimization metaheuristics are proposed and applied for a variety of problems. Cohort Intelligence (CI) algorithm is a socio inspired optimization technique which is successfully applied for solving several unconstrained & constrained real-world problems from the domains such as design, manufacturing, supply chain, healthcare, etc. Generally, real-world problems are constrained in nature. Even though most of the Evolutionary Algorithms (EAs) can efficiently solve unconstrained problems, their performance degenerates when the constraints are involved. In this paper, two novel constraint handling approaches based on modulus and hyperbolic tangent probability distributions are proposed. Constrained CI algorithm with constraint handling approaches based on triangular, modulus and hyperbolic tangent is presented and applied for optimizing advanced manufacturing processes such as Water Jet Machining (WJM), Abrasive Jet Machining (AJM), Ultrasonic Machining (USM) and Grinding process. The solutions obtained using proposed CI algorithm are compared with contemporary algorithms such as Genetic Algorithm, Simulated Annealing, Teaching Learning Based Optimization, etc. The proposed approaches achieved 2%-127% maximization of material removal rate satisfying hard constraints. As compared to the GA, CI with Hyperbolic tangent probability distribution achieved 15%, 2%, 2%, 127%, and 4% improvement in MRR for AJMB, AJMD, WJM, USM, and Grinding processes, respectively contributing to the productivity improvement. The contributions in this paper have opened several avenues for further applicability of the proposed constraint handling approaches for solving complex constrained problems.

LAB: A Leader-Advocate-Believer Based Optimization Algorithm

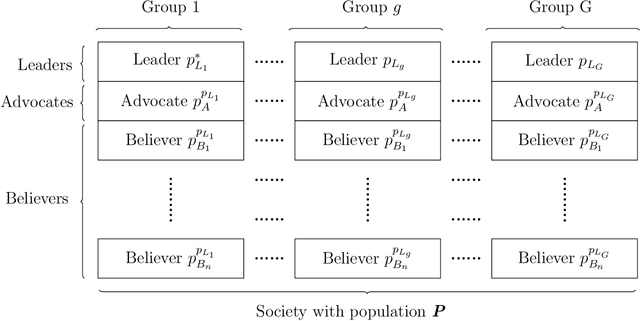
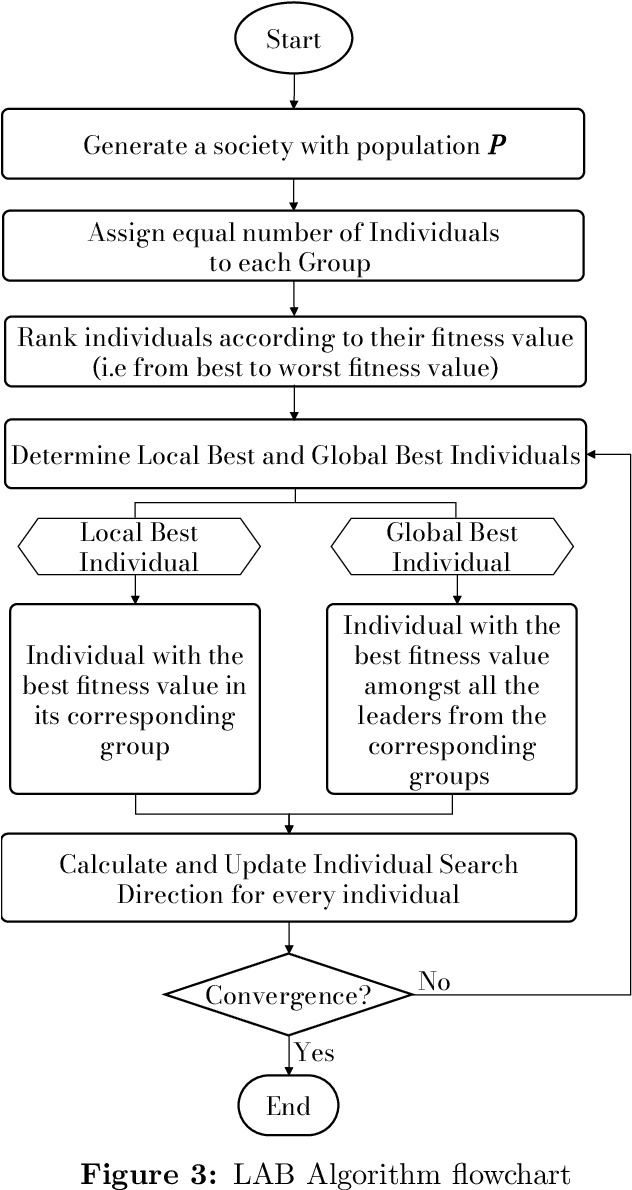
This manuscript introduces a new socio-inspired metaheuristic technique referred to as Leader-Advocate-Believer based optimization algorithm (LAB) for engineering and global optimization problems. The proposed algorithm is inspired by the AI-based competitive behaviour exhibited by the individuals in a group while simultaneously improving themselves and establishing a role (Leader, Advocate, Believer). LAB performance in computational time and function evaluations are benchmarked using other metaheuristic algorithms. Besides benchmark problems, the LAB algorithm was applied for solving challenging engineering problems, including abrasive water jet machining, electric discharge machining, micro-machining processes, and process parameter optimization for turning titanium alloy in a minimum quantity lubrication environment. The results were superior to the other algorithms compared such as Firefly Algorithm, Variations of Co-hort Intelligence, Genetic Algorithm, Simulated Annealing, Particle Swarm Optimisation, and Multi-Cohort Intelligence. The results from this study highlighted that the LAB outperforms the other algorithms in terms of function evaluations and computational time. The prominent features of the LAB algorithm along with its limitations are also discussed.

Multi-Cohort Intelligence Algorithm: An Intra- and Inter-group Learning Behavior based Socio-inspired Optimization Methodology

A Multi-Cohort Intelligence (Multi-CI) metaheuristic algorithm in emerging socio-inspired optimization domain is proposed. The algorithm implements intra-group and inter-group learning mechanisms. It focusses on the interaction amongst different cohorts. The performance of the algorithm is validated by solving 75 unconstrained test problems with dimensions up to 30. The solutions were comparing with several recent algorithms such as Particle Swarm Optimization, Covariance Matrix Adaptation Evolution Strategy, Artificial Bee Colony, Self-adaptive differential evolution algorithm, Comprehensive Learning Particle Swarm Optimization, Backtracking Search Optimization Algorithm and Ideology Algorithm. The Wilcoxon signed rank test was carried out for the statistical analysis and verification of the performance. The proposed Multi-CI outperformed these algorithms in terms of the solution quality including objective function value and computational cost, i.e. computational time and functional evaluations. The prominent feature of the Multi-CI algorithm along with the limitations are discussed as well. In addition, an illustrative example is also solved and every detail is provided.