Dirichlet process mixtures of block $g$ priors for model selection and prediction in linear models

This paper introduces Dirichlet process mixtures of block $g$ priors for model selection and prediction in linear models. These priors are extensions of traditional mixtures of $g$ priors that allow for differential shrinkage for various (data-selected) blocks of parameters while fully accounting for the predictors' correlation structure, providing a bridge between the literatures on model selection and continuous shrinkage priors. We show that Dirichlet process mixtures of block $g$ priors are consistent in various senses and, in particular, that they avoid the conditional Lindley ``paradox'' highlighted by Som et al.(2016). Further, we develop a Markov chain Monte Carlo algorithm for posterior inference that requires only minimal ad-hoc tuning. Finally, we investigate the empirical performance of the prior in various real and simulated datasets. In the presence of a small number of very large effects, Dirichlet process mixtures of block $g$ priors lead to higher power for detecting smaller but significant effects without only a minimal increase in the number of false discoveries.

Small-Variance Asymptotics for Nonparametric Bayesian Overlapping Stochastic Blockmodels

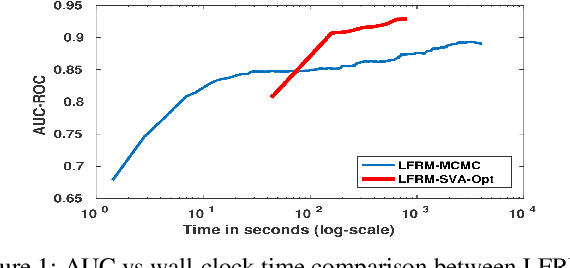
The latent feature relational model (LFRM) is a generative model for graph-structured data to learn a binary vector representation for each node in the graph. The binary vector denotes the node's membership in one or more communities. At its core, the LFRM miller2009nonparametric is an overlapping stochastic blockmodel, which defines the link probability between any pair of nodes as a bilinear function of their community membership vectors. Moreover, using a nonparametric Bayesian prior (Indian Buffet Process) enables learning the number of communities automatically from the data. However, despite its appealing properties, inference in LFRM remains a challenge and is typically done via MCMC methods. This can be slow and may take a long time to converge. In this work, we develop a small-variance asymptotics based framework for the non-parametric Bayesian LFRM. This leads to an objective function that retains the nonparametric Bayesian flavor of LFRM, while enabling us to design deterministic inference algorithms for this model, that are easy to implement (using generic or specialized optimization routines) and are fast in practice. Our results on several benchmark datasets demonstrate that our algorithm is competitive to methods such as MCMC, while being much faster.