Learning with distributional inverters

We generalize the "indirect learning" technique of Furst et. al., 1991 to reduce from learning a concept class over a samplable distribution $\mu$ to learning the same concept class over the uniform distribution. The reduction succeeds when the sampler for $\mu$ is both contained in the target concept class and efficiently invertible in the sense of Impagliazzo & Luby, 1989. We give two applications. - We show that AC0[q] is learnable over any succinctly-described product distribution. AC0[q] is the class of constant-depth Boolean circuits of polynomial size with AND, OR, NOT, and counting modulo $q$ gates of unbounded fanins. Our algorithm runs in randomized quasi-polynomial time and uses membership queries. - If there is a strongly useful natural property in the sense of Razborov & Rudich 1997 -- an efficient algorithm that can distinguish between random strings and strings of non-trivial circuit complexity -- then general polynomial-sized Boolean circuits are learnable over any efficiently samplable distribution in randomized polynomial time, given membership queries to the target function

GANs & Reels: Creating Irish Music using a Generative Adversarial Network

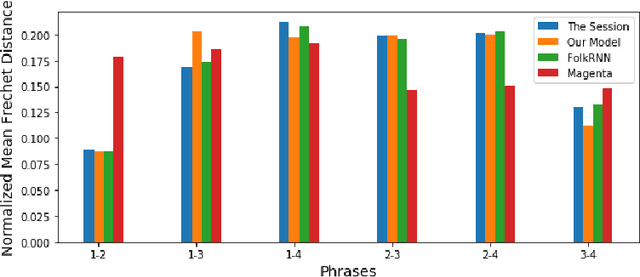
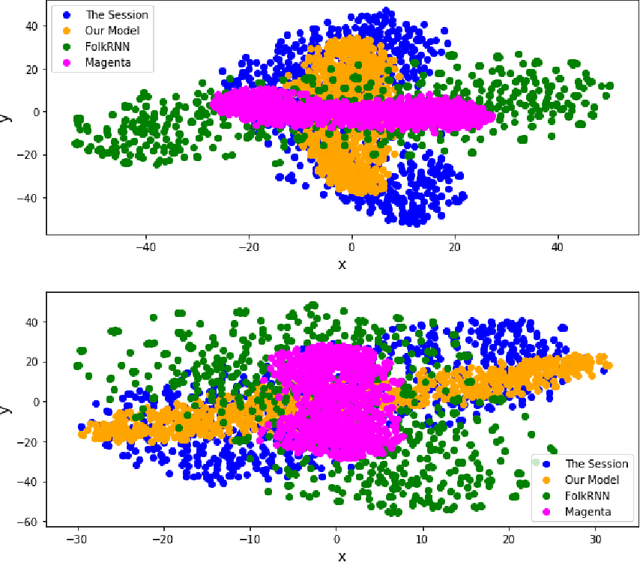
In this paper we present a method for algorithmic melody generation using a generative adversarial network without recurrent components. Music generation has been successfully done using recurrent neural networks, where the model learns sequence information that can help create authentic sounding melodies. Here, we use DC-GAN architecture with dilated convolutions and towers to capture sequential information as spatial image information, and learn long-range dependencies in fixed-length melody forms such as Irish traditional reel.

Approximating solution structure of the Weighted Sentence Alignment problem

We study the complexity of approximating solution structure of the bijective weighted sentence alignment problem of DeNero and Klein (2008). In particular, we consider the complexity of finding an alignment that has a significant overlap with an optimal alignment. We discuss ways of representing the solution for the general weighted sentence alignment as well as phrases-to-words alignment problem, and show that computing a string which agrees with the optimal sentence partition on more than half (plus an arbitrarily small polynomial fraction) positions for the phrases-to-words alignment is NP-hard. For the general weighted sentence alignment we obtain such bound from the agreement on a little over 2/3 of the bits. Additionally, we generalize the Hamming distance approximation of a solution structure to approximating it with respect to the edit distance metric, obtaining similar lower bounds.