Pre-print: Radio Identity Verification-based IoT Security Using RF-DNA Fingerprints and SVM

It is estimated that the number of IoT devices will reach 75 billion in the next five years. Most of those currently, and to be deployed, lack sufficient security to protect themselves and their networks from attack by malicious IoT devices that masquerade as authorized devices to circumvent digital authentication approaches. This work presents a PHY layer IoT authentication approach capable of addressing this critical security need through the use of feature reduced Radio Frequency-Distinct Native Attributes (RF-DNA) fingerprints and Support Vector Machines (SVM). This work successfully demonstrates 100%: (i) authorized ID verification across three trials of six randomly chosen radios at signal-to-noise ratios greater than or equal to 6 dB, and (ii) rejection of all rogue radio ID spoofing attacks at signal-to-noise ratios greater than or equal to 3 dB using RF-DNA fingerprints whose features are selected using the Relief-F algorithm.

dMath: A Scalable Linear Algebra and Math Library for Heterogeneous GP-GPU Architectures

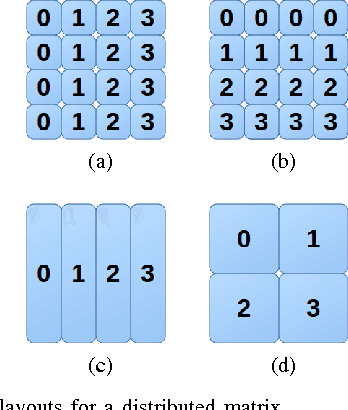
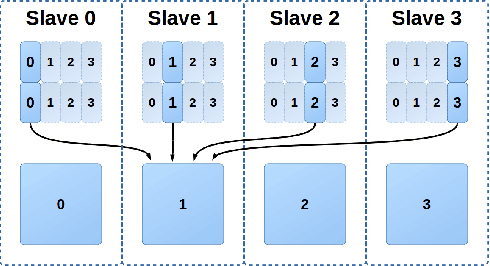
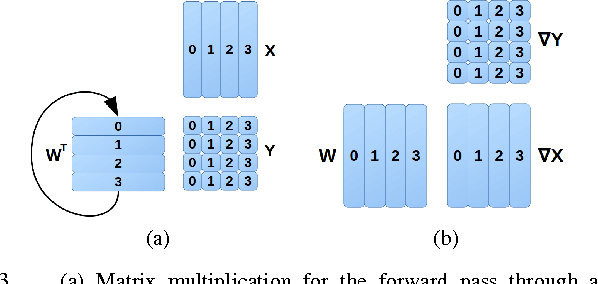
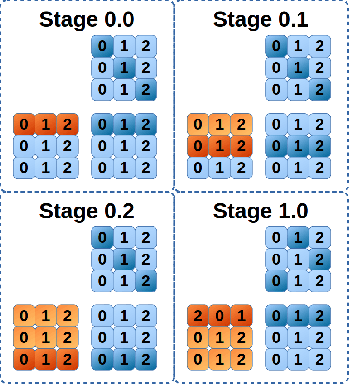
A new scalable parallel math library, dMath, is presented in this paper that demonstrates leading scaling when using intranode, or internode, hybrid-parallelism for deep-learning. dMath provides easy-to-use distributed base primitives and a variety of domain-specific algorithms. These include matrix multiplication, convolutions, and others allowing for rapid development of highly scalable applications, including Deep Neural Networks (DNN), whereas previously one was restricted to libraries that provided effective primitives for only a single GPU, like Nvidia cublas and cudnn or DNN primitives from Nervana neon framework. Development of HPC software is difficult, labor-intensive work, requiring a unique skill set. dMath allows a wide range of developers to utilize parallel and distributed hardware easily. One contribution of this approach is that data is stored persistently on the GPU hardware, avoiding costly transfers between host and device. Advanced memory management techniques are utilized, including caching of transferred data and memory reuse through pooling. A key contribution of dMath is that it delivers performance, portability, and productivity to its specific domain of support. It enables algorithm and application programmers to quickly solve problems without managing the significant complexity associated with multi-level parallelism.