Anthony O. Smith
A Spectral Enabled GAN for Time Series Data Generation
Mar 02, 2021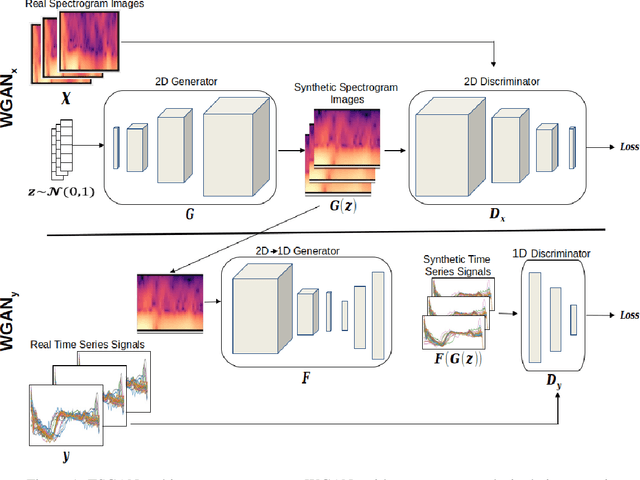
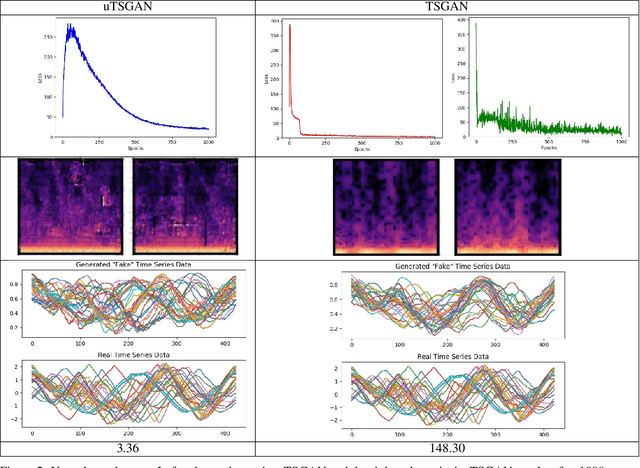
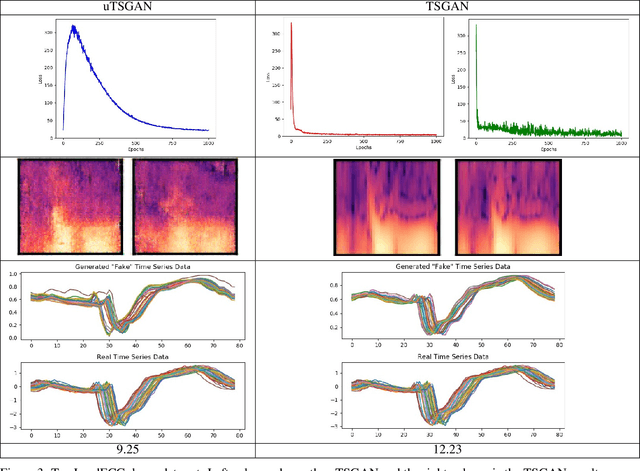
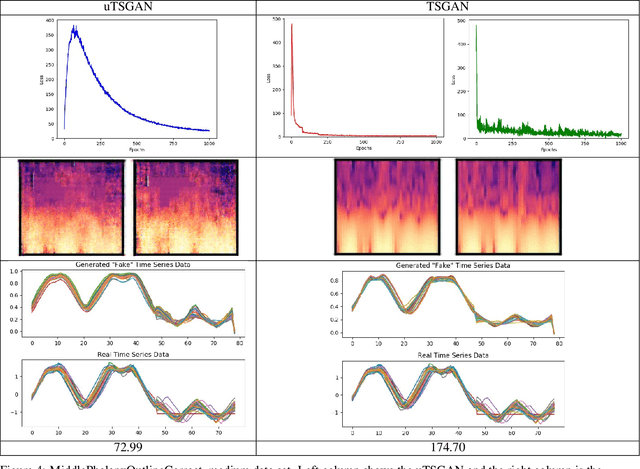
Abstract:Time dependent data is a main source of information in today's data driven world. Generating this type of data though has shown its challenges and made it an interesting research area in the field of generative machine learning. One such approach was that by Smith et al. who developed Time Series Generative Adversarial Network (TSGAN) which showed promising performance in generating time dependent data and the ability of few shot generation though being flawed in certain aspects of training and learning. This paper looks to improve on the results from TSGAN and address those flaws by unifying the training of the independent networks in TSGAN and creating a dependency both in training and learning. This improvement, called unified TSGAN (uTSGAN) was tested and comapred both quantitatively and qualitatively to its predecessor on 70 benchmark time series data sets used in the community. uTSGAN showed to outperform TSGAN in 80\% of the data sets by the same number of training epochs and 60\% of the data sets in 3/4th the amount of training time or less while maintaining the few shot generation ability with better FID scores across those data sets.
A Category Space Approach to Supervised Dimensionality Reduction
Oct 27, 2016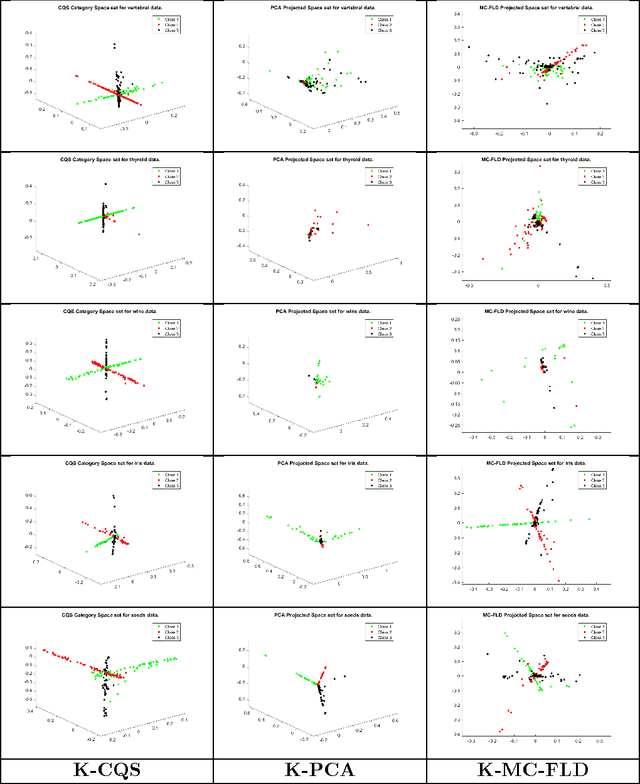
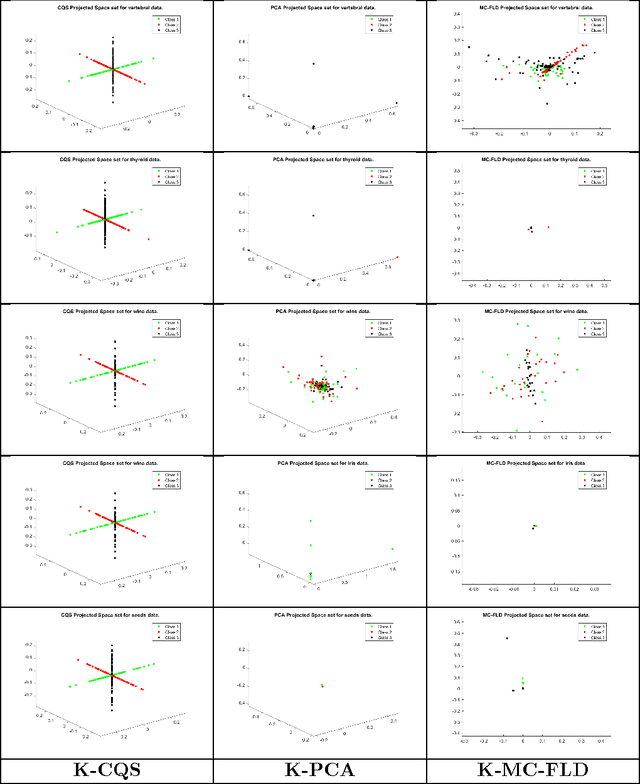
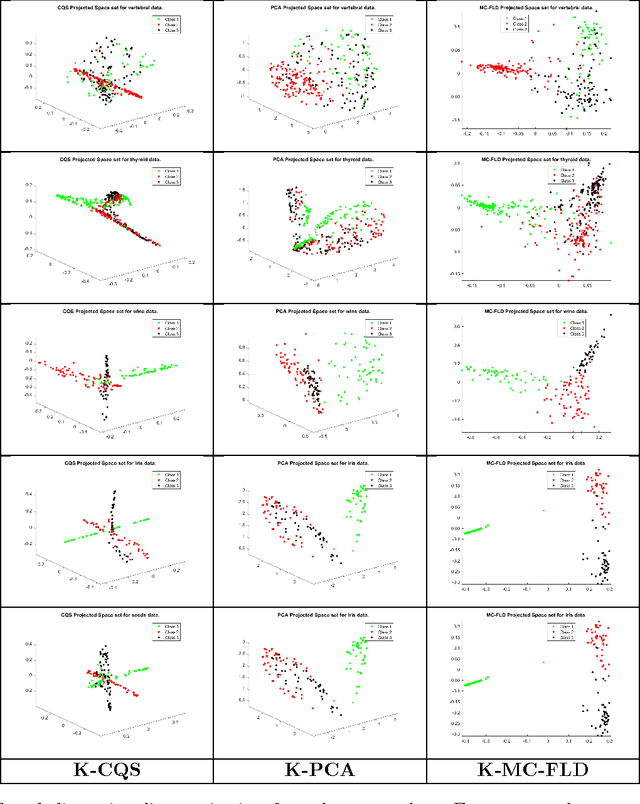
Abstract:Supervised dimensionality reduction has emerged as an important theme in the last decade. Despite the plethora of models and formulations, there is a lack of a simple model which aims to project the set of patterns into a space defined by the classes (or categories). To this end, we set up a model in which each class is represented as a 1D subspace of the vector space formed by the features. Assuming the set of classes does not exceed the cardinality of the features, the model results in multi-class supervised learning in which the features of each class are projected into the class subspace. Class discrimination is automatically guaranteed via the imposition of orthogonality of the 1D class sub-spaces. The resulting optimization problem - formulated as the minimization of a sum of quadratic functions on a Stiefel manifold - while being non-convex (due to the constraints), nevertheless has a structure for which we can identify when we have reached a global minimum. After formulating a version with standard inner products, we extend the formulation to reproducing kernel Hilbert spaces in a straightforward manner. The optimization approach also extends in a similar fashion to the kernel version. Results and comparisons with the multi-class Fisher linear (and kernel) discriminants and principal component analysis (linear and kernel) showcase the relative merits of this approach to dimensionality reduction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge