Innovation Capacity of Dynamical Learning Systems

In noisy physical reservoirs, the classical information-processing capacity $C_{\mathrm{ip}}$ quantifies how well a linear readout can realize tasks measurable from the input history, yet $C_{\mathrm{ip}}$ can be far smaller than the observed rank of the readout covariance. We explain this ``missing capacity'' by introducing the innovation capacity $C_{\mathrm{i}}$, the total capacity allocated to readout components orthogonal to the input filtration (Doob innovations, including input-noise mixing). Using a basis-free Hilbert-space formulation of the predictable/innovation decomposition, we prove the conservation law $C_{\mathrm{ip}}+C_{\mathrm{i}}=\mathrm{rank}(Σ_{XX})\le d$, so predictable and innovation capacities exactly partition the rank of the observable readout dimension covariance $Σ_{XX}\in \mathbb{R}^{\rm d\times d}$. In linear-Gaussian Johnson-Nyquist regimes, $Σ_{XX}(T)=S+T N_0$, the split becomes a generalized-eigenvalue shrinkage rule and gives an explicit monotone tradeoff between temperature and predictable capacity. Geometrically, in whitened coordinates the predictable and innovation components correspond to complementary covariance ellipsoids, making $C_{\mathrm{i}}$ a trace-controlled innovation budget. A large $C_{\mathrm{i}}$ forces a high-dimensional innovation subspace with a variance floor and under mild mixing and anti-concentration assumptions this yields extensive innovation-block differential entropy and exponentially many distinguishable histories. Finally, we give an information-theoretic lower bound showing that learning the induced innovation-block law in total variation requires a number of samples that scales with the effective innovation dimension, supporting the generative utility of noisy physical reservoirs.

Practical Efficiency of Muon for Pretraining

We demonstrate that Muon, the simplest instantiation of a second-order optimizer, explicitly expands the Pareto frontier over AdamW on the compute-time tradeoff. We find that Muon is more effective than AdamW in retaining data efficiency at large batch sizes, far beyond the so-called critical batch size, while remaining computationally efficient, thus enabling more economical training. We study the combination of Muon and the maximal update parameterization (muP) for efficient hyperparameter transfer and present a simple telescoping algorithm that accounts for all sources of error in muP while introducing only a modest overhead in resources. We validate our findings through extensive experiments with model sizes up to four billion parameters and ablations on the data distribution and architecture.

Limits to Reservoir Learning

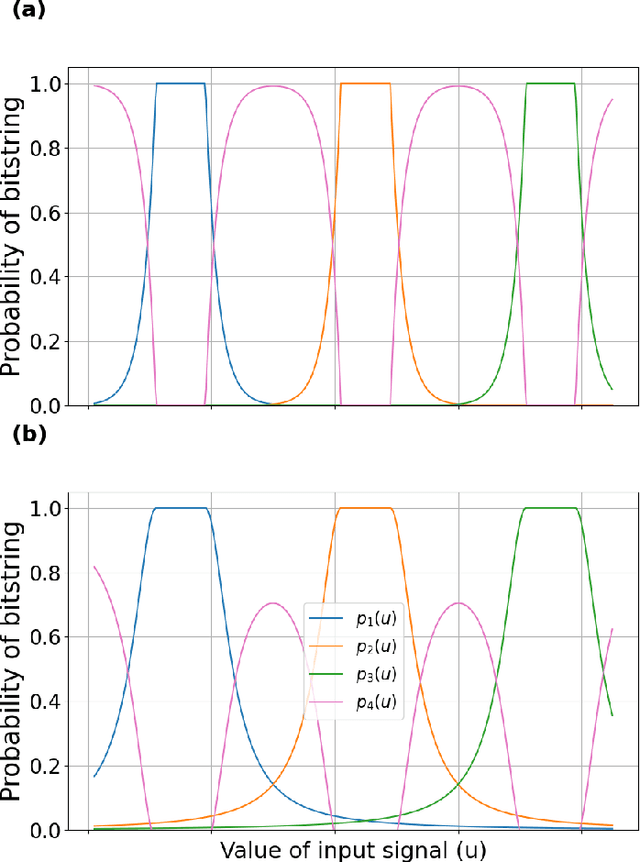
In this work, we bound a machine's ability to learn based on computational limitations implied by physicality. We start by considering the information processing capacity (IPC), a normalized measure of the expected squared error of a collection of signals to a complete basis of functions. We use the IPC to measure the degradation under noise of the performance of reservoir computers, a particular kind of recurrent network, when constrained by physical considerations. First, we show that the IPC is at most a polynomial in the system size $n$, even when considering the collection of $2^n$ possible pointwise products of the $n$ output signals. Next, we argue that this degradation implies that the family of functions represented by the reservoir requires an exponential number of samples to learn in the presence of the reservoir's noise. Finally, we conclude with a discussion of the performance of the same collection of $2^n$ functions without noise when being used for binary classification.

A Note on Noisy Reservoir Computation

In this note we extend the definition of the Information Processing Capacity (IPC) by Dambre et al [1] to include the effects of stochastic reservoir dynamics. We quantify the degradation of the IPC in the presence of this noise. [1] Dambre et al. Scientific Reports 2, 514, (2012)