Singular-limit analysis of gradient descent with noise injection

We study the limiting dynamics of a large class of noisy gradient descent systems in the overparameterized regime. In this regime the set of global minimizers of the loss is large, and when initialized in a neighbourhood of this zero-loss set a noisy gradient descent algorithm slowly evolves along this set. In some cases this slow evolution has been related to better generalisation properties. We characterize this evolution for the broad class of noisy gradient descent systems in the limit of small step size. Our results show that the structure of the noise affects not just the form of the limiting process, but also the time scale at which the evolution takes place. We apply the theory to Dropout, label noise and classical SGD (minibatching) noise, and show that these evolve on different two time scales. Classical SGD even yields a trivial evolution on both time scales, implying that additional noise is required for regularization. The results are inspired by the training of neural networks, but the theorems apply to noisy gradient descent of any loss that has a non-trivial zero-loss set.

Tensorized Transformer for Dynamical Systems Modeling

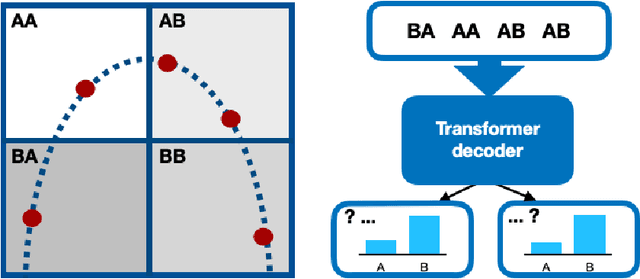
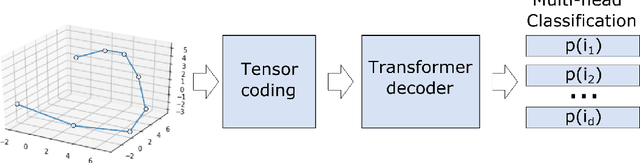
The identification of nonlinear dynamics from observations is essential for the alignment of the theoretical ideas and experimental data. The last, in turn, is often corrupted by the side effects and noise of different natures, so probabilistic approaches could give a more general picture of the process. At the same time, high-dimensional probabilities modeling is a challenging and data-intensive task. In this paper, we establish a parallel between the dynamical systems modeling and language modeling tasks. We propose a transformer-based model that incorporates geometrical properties of the data and provide an iterative training algorithm allowing the fine-grid approximation of the conditional probabilities of high-dimensional dynamical systems.

Deep Representation Learning for Dynamical Systems Modeling

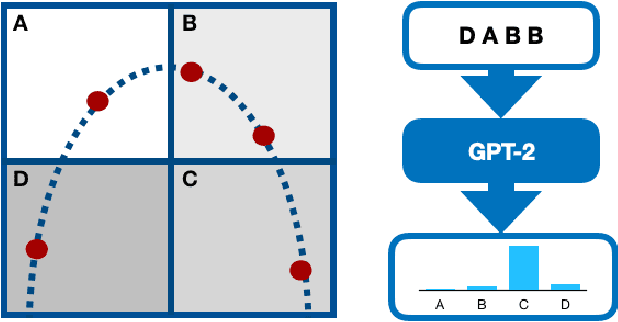
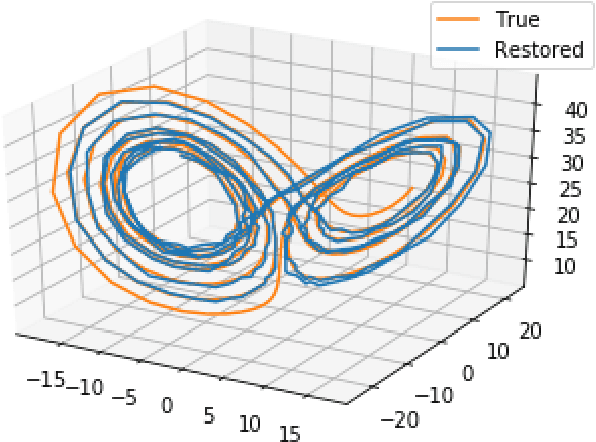
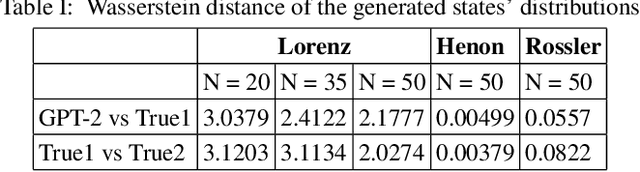
Proper states' representations are the key to the successful dynamics modeling of chaotic systems. Inspired by recent advances of deep representations in various areas such as natural language processing and computer vision, we propose the adaptation of the state-of-art Transformer model in application to the dynamical systems modeling. The model demonstrates promising results in trajectories generation as well as in the general attractors' characteristics approximation, including states' distribution and Lyapunov exponent.