Tensorized Transformer for Dynamical Systems Modeling

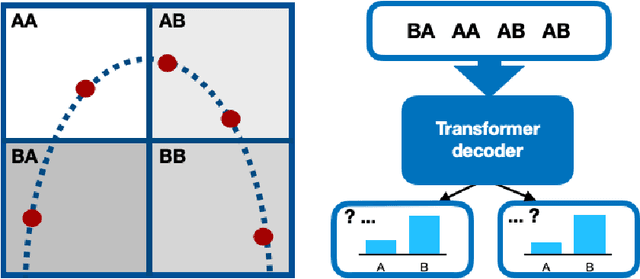
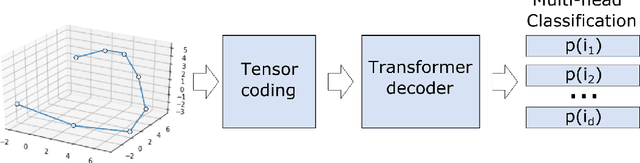
The identification of nonlinear dynamics from observations is essential for the alignment of the theoretical ideas and experimental data. The last, in turn, is often corrupted by the side effects and noise of different natures, so probabilistic approaches could give a more general picture of the process. At the same time, high-dimensional probabilities modeling is a challenging and data-intensive task. In this paper, we establish a parallel between the dynamical systems modeling and language modeling tasks. We propose a transformer-based model that incorporates geometrical properties of the data and provide an iterative training algorithm allowing the fine-grid approximation of the conditional probabilities of high-dimensional dynamical systems.