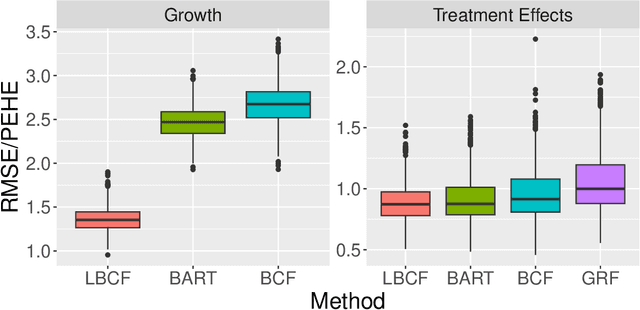
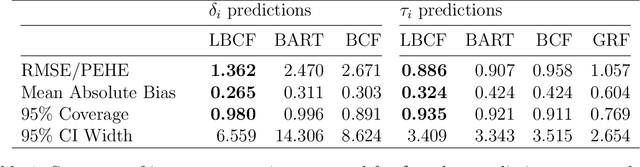
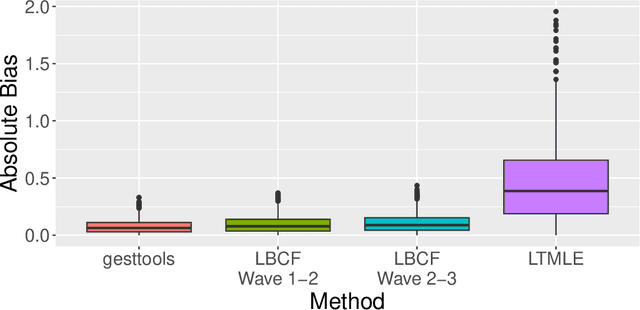
Bayesian Causal Forests for Longitudinal Data: Assessing the Impact of Part-Time Work on Growth in High School Mathematics Achievement

Modelling growth in student achievement is a significant challenge in the field of education. Understanding how interventions or experiences such as part-time work can influence this growth is also important. Traditional methods like difference-in-differences are effective for estimating causal effects from longitudinal data. Meanwhile, Bayesian non-parametric methods have recently become popular for estimating causal effects from single time point observational studies. However, there remains a scarcity of methods capable of combining the strengths of these two approaches to flexibly estimate heterogeneous causal effects from longitudinal data. Motivated by two waves of data from the High School Longitudinal Study, the NCES' most recent longitudinal study which tracks a representative sample of over 20,000 students in the US, our study introduces a longitudinal extension of Bayesian Causal Forests. This model allows for the flexible identification of both individual growth in mathematical ability and the effects of participation in part-time work. Simulation studies demonstrate the predictive performance and reliable uncertainty quantification of the proposed model. Results reveal the negative impact of part time work for most students, but hint at potential benefits for those students with an initially low sense of school belonging. Clear signs of a widening achievement gap between students with high and low academic achievement are also identified. Potential policy implications are discussed, along with promising areas for future research.

Bayesian Causal Forests for Multivariate Outcomes: Application to Irish Data From an International Large Scale Education Assessment

Bayesian Causal Forests (BCF) is a causal inference machine learning model based on a highly flexible non-parametric regression and classification tool called Bayesian Additive Regression Trees (BART). Motivated by data from the Trends in International Mathematics and Science Study (TIMSS), which includes data on student achievement in both mathematics and science, we present a multivariate extension of the BCF algorithm. With the help of simulation studies we show that our approach can accurately estimate causal effects for multiple outcomes subject to the same treatment. We also apply our model to Irish data from TIMSS 2019. Our findings reveal the positive effects of having access to a study desk at home (Mathematics ATE 95% CI: [0.20, 11.67]) while also highlighting the negative consequences of students often feeling hungry at school (Mathematics ATE 95% CI: [-11.15, -2.78] , Science ATE 95% CI: [-10.82,-1.72]) or often being absent (Mathematics ATE 95% CI: [-12.47, -1.55]).

Semi-parametric Bayesian Additive Regression Trees

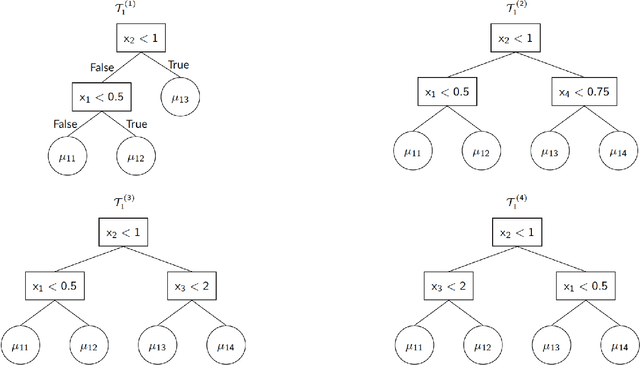
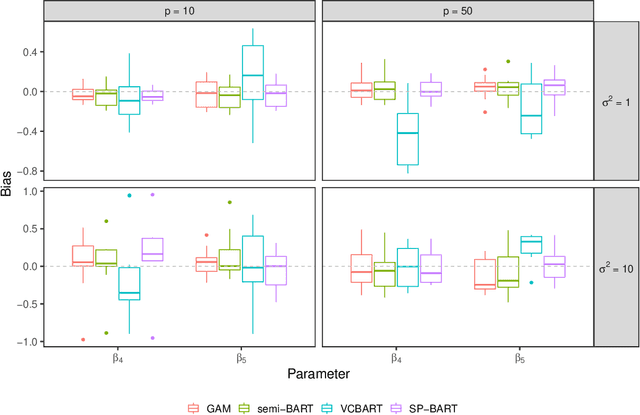
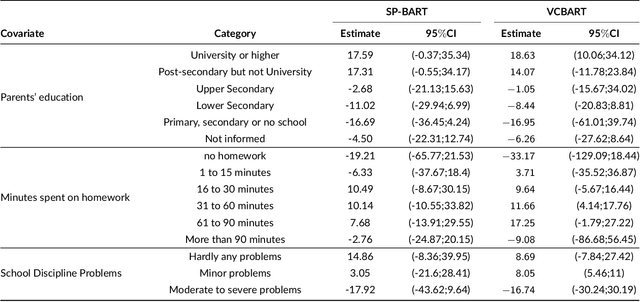
We propose a new semi-parametric model based on Bayesian Additive Regression Trees (BART). In our approach, the response variable is approximated by a linear predictor and a BART model, where the first component is responsible for estimating the main effects and BART accounts for the non-specified interactions and non-linearities. The novelty in our approach lies in the way we change tree generation moves in BART to deal with confounding between the parametric and non-parametric components when they have covariates in common. Through synthetic and real-world examples, we demonstrate that the performance of the new semi-parametric BART is competitive when compared to regression models and other tree-based methods. The implementation of the proposed method is available at https://github.com/ebprado/SP-BART.