In-situ Stochastic Training of MTJ Crossbar based Neural Networks

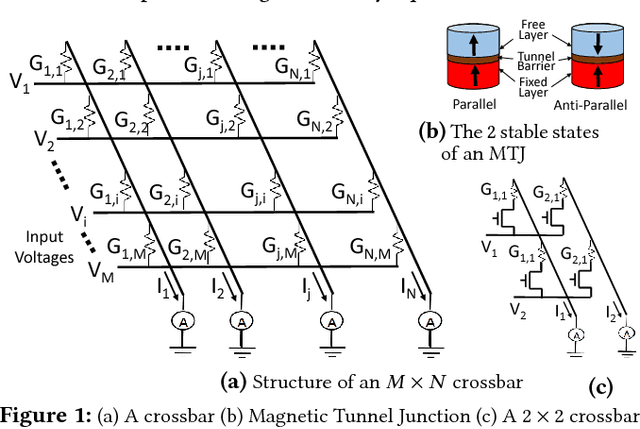
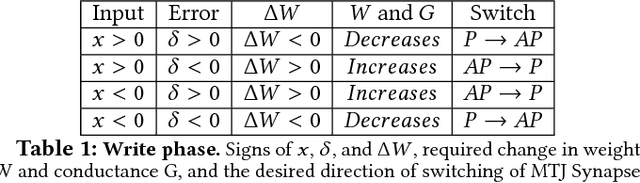
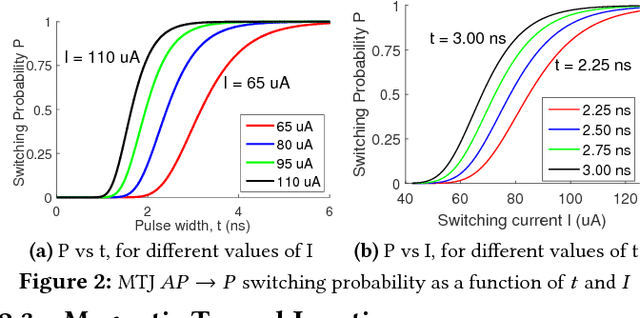
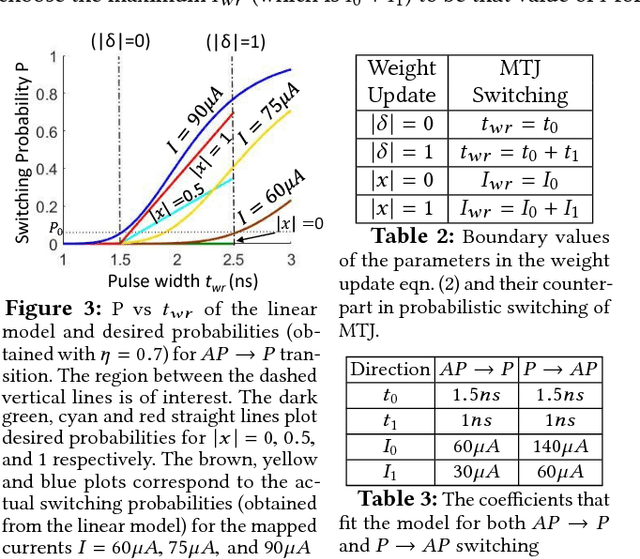
Owing to high device density, scalability and non-volatility, Magnetic Tunnel Junction-based crossbars have garnered significant interest for implementing the weights of an artificial neural network. The existence of only two stable states in MTJs implies a high overhead of obtaining optimal binary weights in software. We illustrate that the inherent parallelism in the crossbar structure makes it highly appropriate for in-situ training, wherein the network is taught directly on the hardware. It leads to significantly smaller training overhead as the training time is independent of the size of the network, while also circumventing the effects of alternate current paths in the crossbar and accounting for manufacturing variations in the device. We show how the stochastic switching characteristics of MTJs can be leveraged to perform probabilistic weight updates using the gradient descent algorithm. We describe how the update operations can be performed on crossbars both with and without access transistors and perform simulations on them to demonstrate the effectiveness of our techniques. The results reveal that stochastically trained MTJ-crossbar NNs achieve a classification accuracy nearly same as that of real-valued-weight networks trained in software and exhibit immunity to device variations.

Power Optimizations in MTJ-based Neural Networks through Stochastic Computing

Artificial Neural Networks (ANNs) have found widespread applications in tasks such as pattern recognition and image classification. However, hardware implementations of ANNs using conventional binary arithmetic units are computationally expensive, energy-intensive and have large area overheads. Stochastic Computing (SC) is an emerging paradigm which replaces these conventional units with simple logic circuits and is particularly suitable for fault-tolerant applications. Spintronic devices, such as Magnetic Tunnel Junctions (MTJs), are capable of replacing CMOS in memory and logic circuits. In this work, we propose an energy-efficient use of MTJs, which exhibit probabilistic switching behavior, as Stochastic Number Generators (SNGs), which forms the basis of our NN implementation in the SC domain. Further, error resilient target applications of NNs allow us to introduce Approximate Computing, a framework wherein accuracy of computations is traded-off for substantial reductions in power consumption. We propose approximating the synaptic weights in our MTJ-based NN implementation, in ways brought about by properties of our MTJ-SNG, to achieve energy-efficiency. We design an algorithm that can perform such approximations within a given error tolerance in a single-layer NN in an optimal way owing to the convexity of the problem formulation. We then use this algorithm and develop a heuristic approach for approximating multi-layer NNs. To give a perspective of the effectiveness of our approach, a 43% reduction in power consumption was obtained with less than 1% accuracy loss on a standard classification problem, with 26% being brought about by the proposed algorithm.