Ankit Chauhan
Approximating Optimization Problems using EAs on Scale-Free Networks
Jun 14, 2017


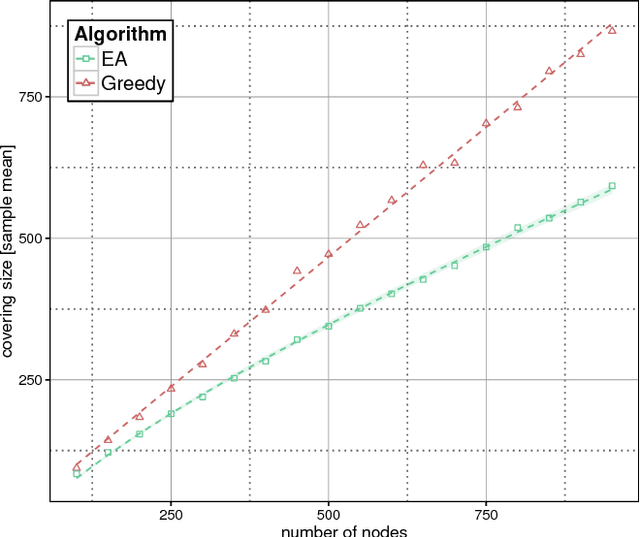
Abstract:It has been experimentally observed that real-world networks follow certain topological properties, such as small-world, power-law etc. To study these networks, many random graph models, such as Preferential Attachment, have been proposed. In this paper, we consider the deterministic properties which capture power-law degree distribution and degeneracy. Networks with these properties are known as scale-free networks in the literature. Many interesting problems remain NP-hard on scale-free networks. We study the relationship between scale-free properties and the approximation-ratio of some commonly used evolutionary algorithms. For the Vertex Cover, we observe experimentally that the (1+1)-EA always gives the better result than a greedy local search, even when it runs for only $\mathcal{O}(n \log (n))$ steps. We give the construction of a scale-free network in which the (1+1)-EA takes $\Omega(n^2)$ steps to obtain a solution as good as the greedy algorithm with constant probability. We prove that for the Dominating Set, Vertex Cover, Connected Dominating Set and Independent Set, the (1+1)-EA obtains constant-factor approximation in expected run time $\mathcal{O}(n \log (n))$ and $\mathcal{O}(n^4)$ respectively. Whereas, the GSEMO gives even better approximation than (1+1)-EA in the expected run time of $\mathcal{O}(n^3)$ for Dominating Set, Vertex Cover and Connected Dominating Set on such networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge