Efficient emotion recognition using hyperdimensional computing with combinatorial channel encoding and cellular automata

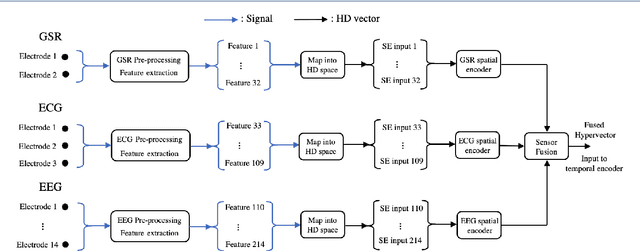
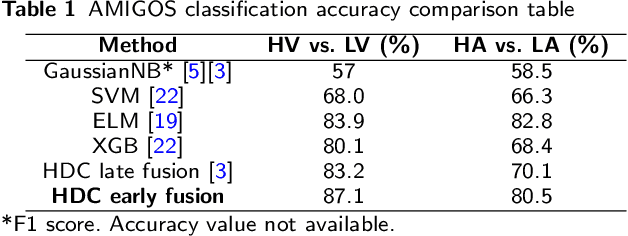
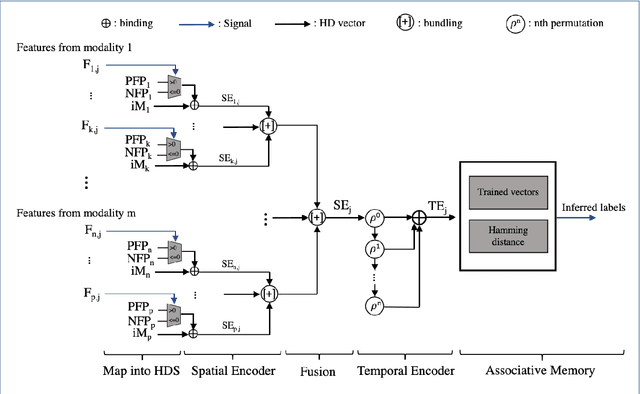
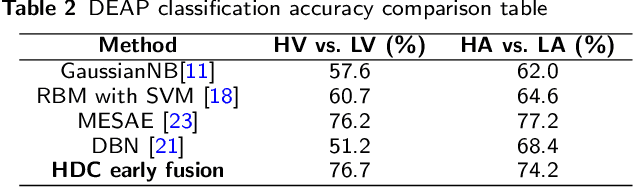
In this paper, a hardware-optimized approach to emotion recognition based on the efficient brain-inspired hyperdimensional computing (HDC) paradigm is proposed. Emotion recognition provides valuable information for human-computer interactions, however the large number of input channels (>200) and modalities (>3) involved in emotion recognition are significantly expensive from a memory perspective. To address this, methods for memory reduction and optimization are proposed, including a novel approach that takes advantage of the combinatorial nature of the encoding process, and an elementary cellular automaton. HDC with early sensor fusion is implemented alongside the proposed techniques achieving two-class multi-modal classification accuracies of >76% for valence and >73% for arousal on the multi-modal AMIGOS and DEAP datasets, almost always better than state of the art. The required vector storage is seamlessly reduced by 98% and the frequency of vector requests by at least 1/5. The results demonstrate the potential of efficient hyperdimensional computing for low-power, multi-channeled emotion recognition tasks.

Active learning workflows and integrable deep neural networks for representing the free energy functions of alloy

The free energy plays a fundamental role in descriptions of many systems in continuum physics. Notably, in multiphysics applications, it encodes thermodynamic coupling between different fields, such as mechanics and chemistry. It thereby gives rise to driving forces on the dynamics of interaction between the constituent phenomena. In mechano-chemically interacting materials systems, even consideration of only compositions, order parameters and strains can render the free energy to be reasonably high-dimensional. In proposing free energy functions as a paradigm for scale bridging, we have previously exploited neural networks for their representation of such high-dimensional functions. Specifically, we have developed an integrable deep neural network (IDNN) that can be trained to free energy derivative data obtained from atomic scale models and statistical mechanics, then analytically integrated to recover a free energy function. The motivation comes from the statistical mechanics formalism, in which certain free energy derivatives are accessible for control of the system, rather than the free energy itself in its entirety. Our current work combines the IDNN with an active learning workflow to improve sampling of the free energy derivative data in a high-dimensional input space. Treated as input-output maps, machine learning representations accommodate role reversals between independent and dependent quantities as the mathematical descriptions change across scale boundaries. As a prototypical material system we focus on Ni-Al. Phase field simulations using the resulting IDNN representation for the free energy of Ni-Al demonstrates that the appropriate physics of the material have been learned.