Generalized Neural Policies for Relational MDPs

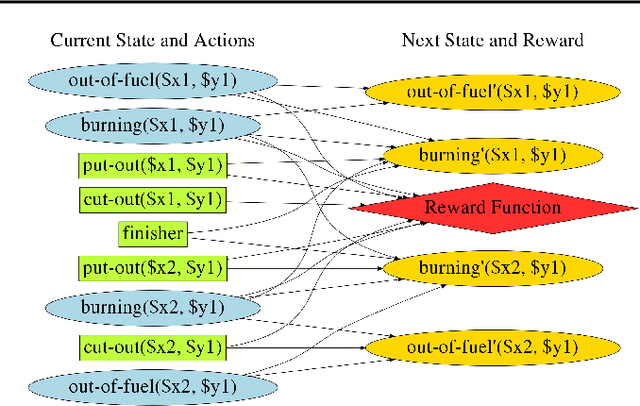
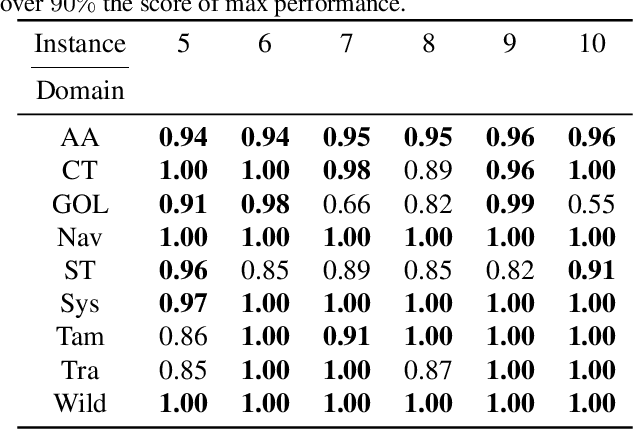
A Relational Markov Decision Process (RMDP) is a first-order representation to express all instances of a single probabilistic planning domain with possibly unbounded number of objects. Early work in RMDPs outputs generalized (instance-independent) first-order policies or value functions as a means to solve all instances of a domain at once. Unfortunately, this line of work met with limited success due to inherent limitations of the representation space used in such policies or value functions. Can neural models provide the missing link by easily representing more complex generalized policies, thus making them effective on all instances of a given domain? We present the first neural approach for solving RMDPs, expressed in the probabilistic planning language of RDDL. Our solution first converts an RDDL instance into a ground DBN. We then extract a graph structure from the DBN. We train a relational neural model that computes an embedding for each node in the graph and also scores each ground action as a function over the first-order action variable and object embeddings on which the action is applied. In essence, this represents a neural generalized policy for the whole domain. Given a new test problem of the same domain, we can compute all node embeddings using trained parameters and score each ground action to choose the best action using a single forward pass without any retraining. Our experiments on nine RDDL domains from IPPC demonstrate that neural generalized policies are significantly better than random and sometimes even more effective than training a state-of-the-art deep reactive policy from scratch.

Size Independent Neural Transfer for RDDL Planning

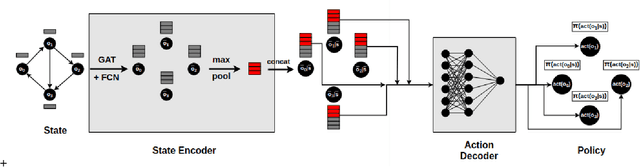
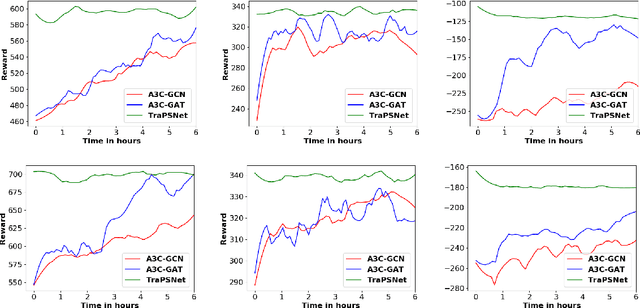
Neural planners for RDDL MDPs produce deep reactive policies in an offline fashion. These scale well with large domains, but are sample inefficient and time-consuming to train from scratch for each new problem. To mitigate this, recent work has studied neural transfer learning, so that a generic planner trained on other problems of the same domain can rapidly transfer to a new problem. However, this approach only transfers across problems of the same size. We present the first method for neural transfer of RDDL MDPs that can transfer across problems of different sizes. Our architecture has two key innovations to achieve size independence: (1) a state encoder, which outputs a fixed length state embedding by max pooling over varying number of object embeddings, (2) a single parameter-tied action decoder that projects object embeddings into action probabilities for the final policy. On the two challenging RDDL domains of SysAdmin and Game Of Life, our approach powerfully transfers across problem sizes and has superior learning curves over training from scratch.

Transfer of Deep Reactive Policies for MDP Planning

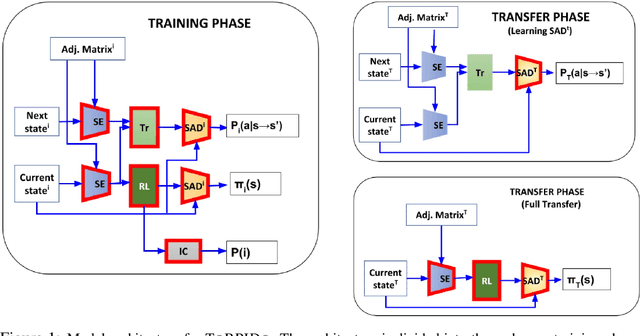
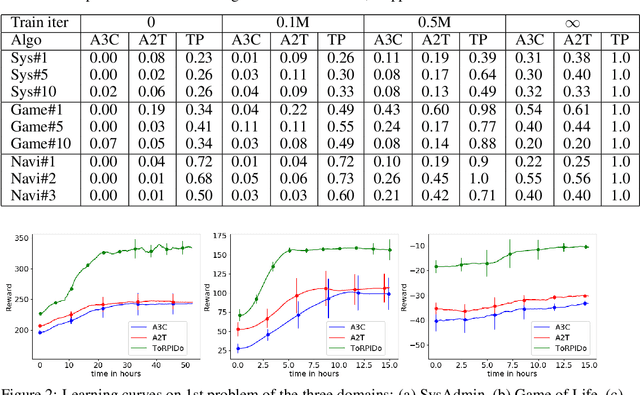
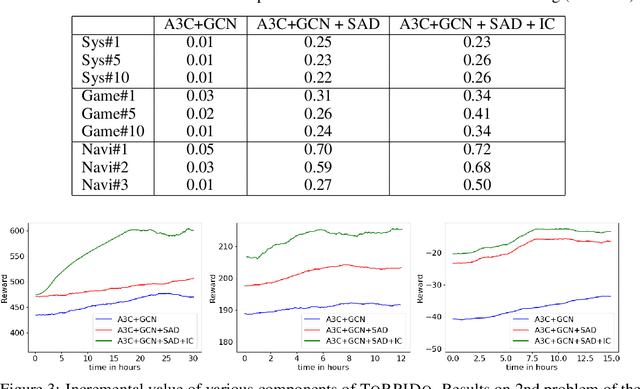
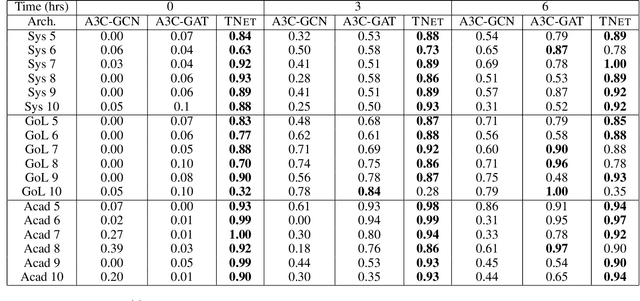
Domain-independent probabilistic planners input an MDP description in a factored representation language such as PPDDL or RDDL, and exploit the specifics of the representation for faster planning. Traditional algorithms operate on each problem instance independently, and good methods for transferring experience from policies of other instances of a domain to a new instance do not exist. Recently, researchers have begun exploring the use of deep reactive policies, trained via deep reinforcement learning (RL), for MDP planning domains. One advantage of deep reactive policies is that they are more amenable to transfer learning. In this paper, we present the first domain-independent transfer algorithm for MDP planning domains expressed in an RDDL representation. Our architecture exploits the symbolic state configuration and transition function of the domain (available via RDDL) to learn a shared embedding space for states and state-action pairs for all problem instances of a domain. We then learn an RL agent in the embedding space, making a near zero-shot transfer possible, i.e., without much training on the new instance, and without using the domain simulator at all. Experiments on three different benchmark domains underscore the value of our transfer algorithm. Compared against planning from scratch, and a state-of-the-art RL transfer algorithm, our transfer solution has significantly superior learning curves.