Generalized Neural Policies for Relational MDPs

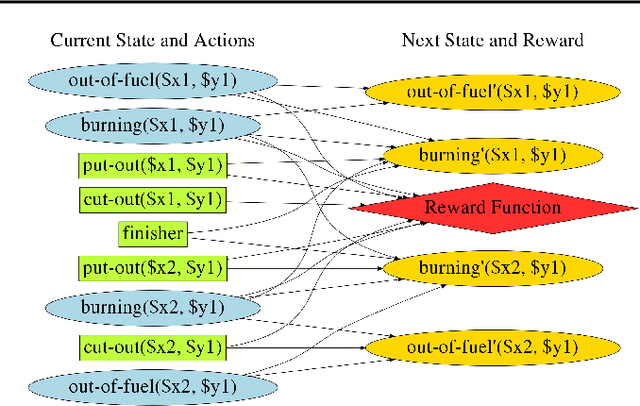
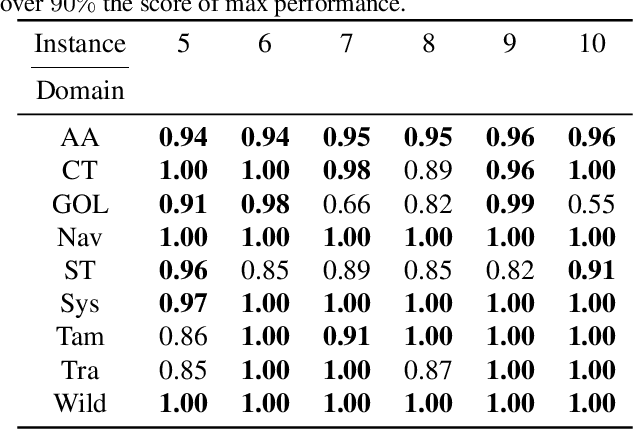
A Relational Markov Decision Process (RMDP) is a first-order representation to express all instances of a single probabilistic planning domain with possibly unbounded number of objects. Early work in RMDPs outputs generalized (instance-independent) first-order policies or value functions as a means to solve all instances of a domain at once. Unfortunately, this line of work met with limited success due to inherent limitations of the representation space used in such policies or value functions. Can neural models provide the missing link by easily representing more complex generalized policies, thus making them effective on all instances of a given domain? We present the first neural approach for solving RMDPs, expressed in the probabilistic planning language of RDDL. Our solution first converts an RDDL instance into a ground DBN. We then extract a graph structure from the DBN. We train a relational neural model that computes an embedding for each node in the graph and also scores each ground action as a function over the first-order action variable and object embeddings on which the action is applied. In essence, this represents a neural generalized policy for the whole domain. Given a new test problem of the same domain, we can compute all node embeddings using trained parameters and score each ground action to choose the best action using a single forward pass without any retraining. Our experiments on nine RDDL domains from IPPC demonstrate that neural generalized policies are significantly better than random and sometimes even more effective than training a state-of-the-art deep reactive policy from scratch.