Divergence-Kernel method for linear responses and diffusion models

We derive the divergence-kernel formula for the linear response (parameter-derivative of marginal or stationary distributions) of random dynamical systems, and formally pass to the continuous-time limit. Our formula works for multiplicative and parameterized noise over any period of time; it does not require hyperbolicity. Then we derive a pathwise Monte-Carlo algorithm for linear responses. With this, we propose a forward-only diffusion generative model and test on simple problems.

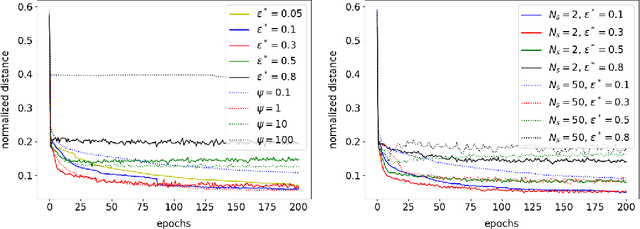
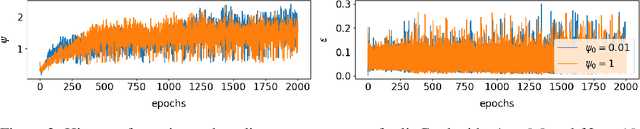
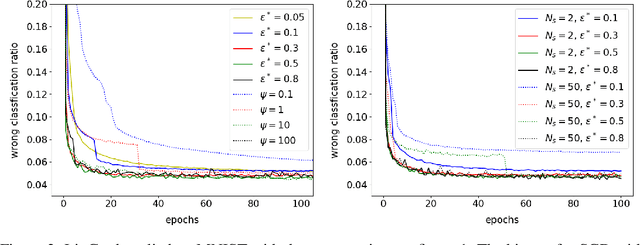
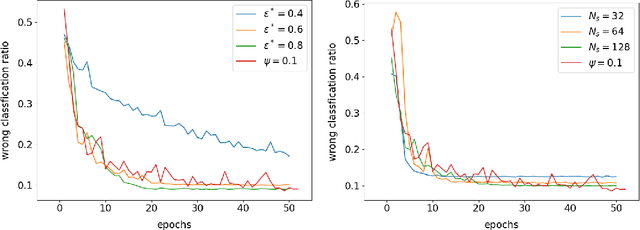
Linear Range in Gradient Descent

This paper defines linear range as the range of parameter perturbations which lead to approximately linear perturbations in the states of a network. We compute linear range from the difference between actual perturbations in states and the tangent solution. Linear range is a new criterion for estimating the effectivenss of gradients and thus having many possible applications. In particular, we propose that the optimal learning rate at the initial stages of training is such that parameter changes on all minibatches are within linear range. We demonstrate our algorithm on two shallow neural networks and a ResNet.