Linear Range in Gradient Descent

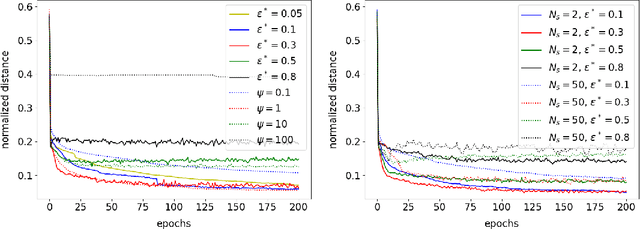
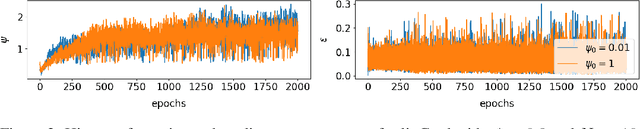
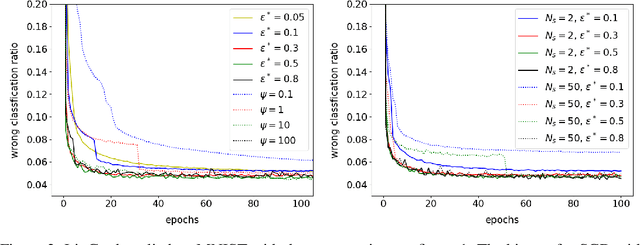
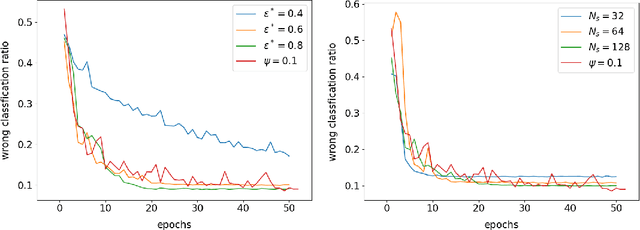
This paper defines linear range as the range of parameter perturbations which lead to approximately linear perturbations in the states of a network. We compute linear range from the difference between actual perturbations in states and the tangent solution. Linear range is a new criterion for estimating the effectivenss of gradients and thus having many possible applications. In particular, we propose that the optimal learning rate at the initial stages of training is such that parameter changes on all minibatches are within linear range. We demonstrate our algorithm on two shallow neural networks and a ResNet.