Angel F. García-Fernández
Set-Type Belief Propagation with Applications to Mapping, MTT, SLAM, and SLAT
May 05, 2023

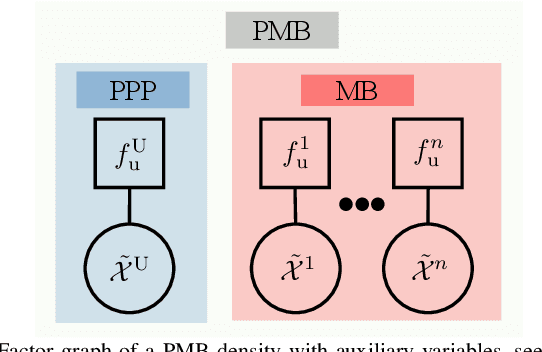
Abstract:Belief propagation (BP) is a useful probabilistic inference algorithm for efficiently computing approximate marginal probability densities of random variables. However, in its standard form, BP is applicable to only the vector-type random variables, while certain applications rely on set-type random variables with an unknown number of vector elements. In this paper, we first develop BP rules for set-type random variables and demonstrate that vector-type BP is a special case of set-type BP. We further propose factor graphs with set-factor and set-variable nodes by devising the set-factor nodes that can address the set-variables with random elements and cardinality, while the number of vector elements in vector-type is known. To demonstrate the validity of developed set-type BP, we apply it to the Poisson multi-Bernoulli (PMB) filter for simultaneous localization and mapping (SLAM), which naturally leads to a new set-type BP-SLAM filter. Finally, we reveal connections between the vector-type BP-SLAM filter and the proposed set-type BP-SLAM filter and show a performance gain of the proposed set-type BP-SLAM filter in comparison with the vector-type BP-SLAM filter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge