Andrey Lokhov
Mobility Map Inference from Thermal Modeling of a Building
Nov 14, 2020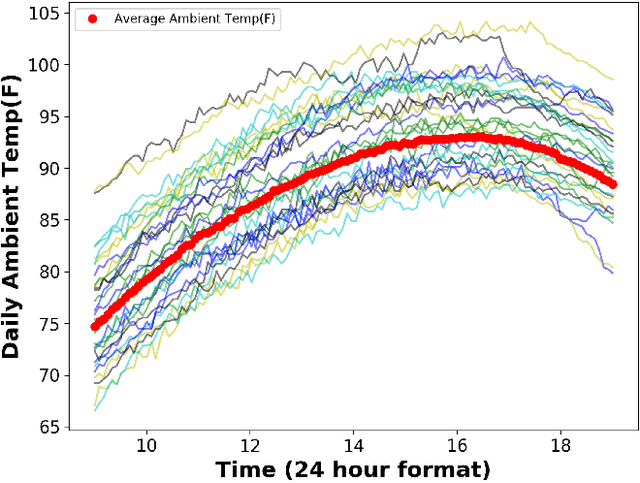
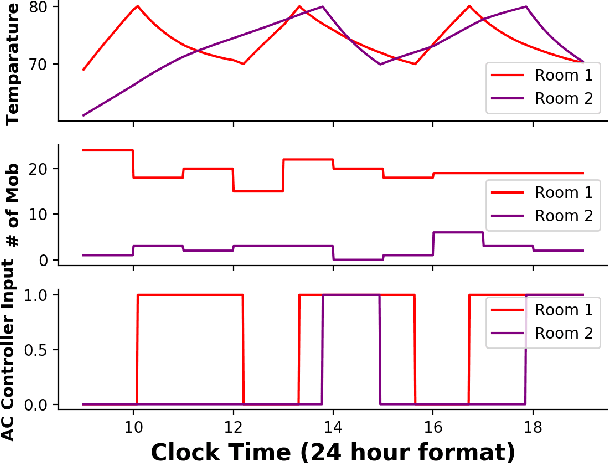

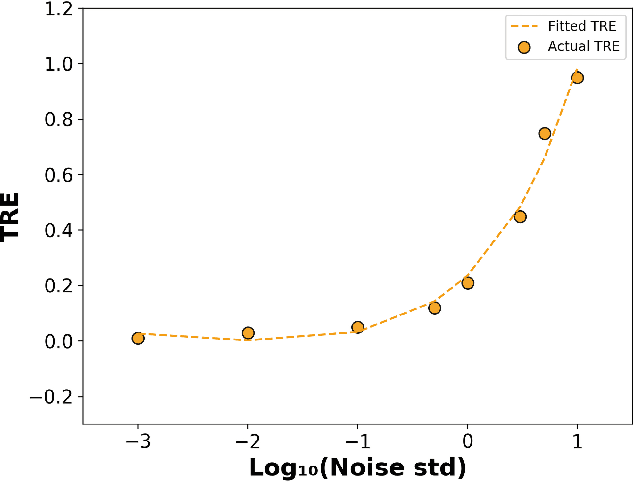
Abstract:We consider the problem of inferring the mobility map, which is the distribution of the building occupants at each timestamp, from the temperatures of the rooms. We also want to explore the effects of noise in the temperature measurement, room layout, etc. in the reconstruction of the movement of people within the building. Our proposed algorithm tackles down the aforementioned challenges leveraging a parameter learner, the modified Least Square Estimator. In the absence of a complete data set with mobility map, room and ambient temperatures, and HVAC data in the public domain, we simulate a physics-based thermal model of the rooms in a building and evaluate the performance of our inference algorithm on this simulated data. We find an upper bound of the noise standard deviation (<= 1F) in the input temperature data of our model. Within this bound, our algorithm can reconstruct the mobility map with a reasonable reconstruction error. Our work can be used in a wide range of applications, for example, ensuring the physical security of office buildings, elderly and infant monitoring, building resources management, emergency building evacuation, and vulnerability assessment of HVAC data. Our work brings together multiple research areas, Thermal Modeling and Parameter Estimation, towards achieving a common goal of inferring the distribution of people within a large office building.
Learning of Discrete Graphical Models with Neural Networks
Jun 21, 2020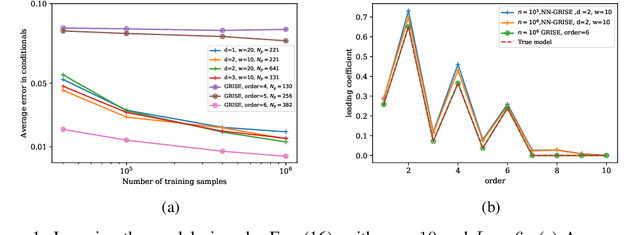
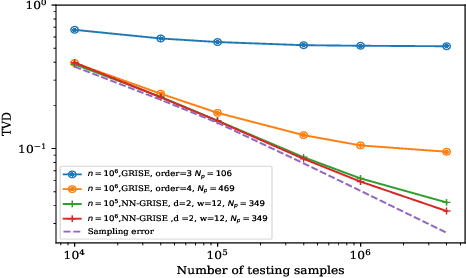
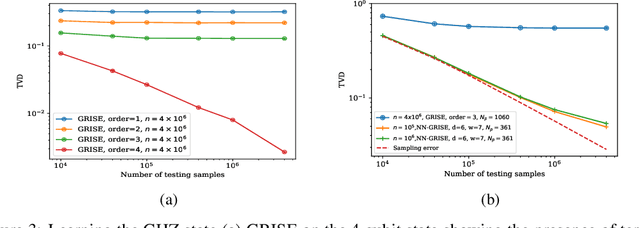
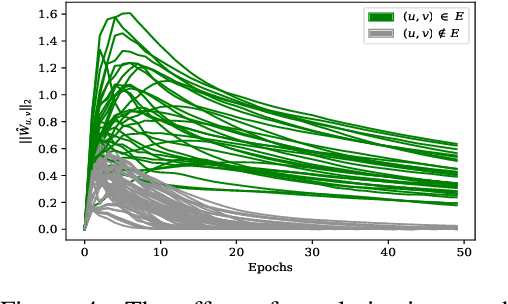
Abstract:Graphical models are widely used in science to represent joint probability distributions with an underlying conditional dependence structure. The inverse problem of learning a discrete graphical model given i.i.d samples from its joint distribution can be solved with near-optimal sample complexity using a convex optimization method known as Generalized Regularized Interaction Screening Estimator (GRISE). But the computational cost of GRISE becomes prohibitive when the energy function of the true graphical model has higher order terms. We introduce NN-GRISE, a neural net based algorithm for graphical model learning, to tackle this limitation of GRISE. We use neural nets as function approximators in an interaction screening objective function. The optimization of this objective then produces a neural-net representation for the conditionals of the graphical model. NN-GRISE algorithm is seen to be a better alternative to GRISE when the energy function of the true model has a high order with a high degree of symmetry. In these cases, NN-GRISE is able to find the correct parsimonious representation for the conditionals without being fed any prior information about the true model. NN-GRISE can also be used to learn the underlying structure of the true model with some simple modifications to its training procedure. In addition, we also show a variant of NN-GRISE that can be used to learn a neural net representation for the full energy function of the true model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge