A persistent homology-based topological loss for CNN-based multi-class segmentation of CMR

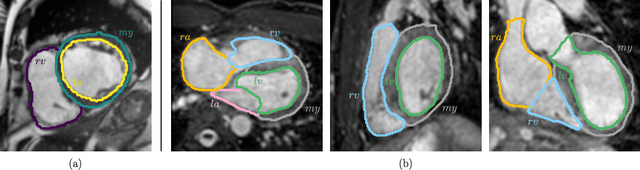
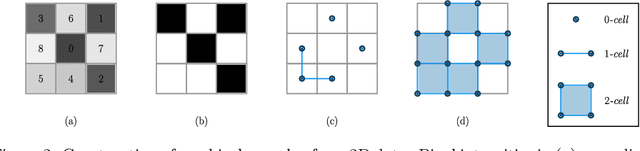
Multi-class segmentation of cardiac magnetic resonance (CMR) images seeks a separation of data into anatomical components with known structure and configuration. The most popular CNN-based methods are optimised using pixel wise loss functions, ignorant of the spatially extended features that characterise anatomy. Therefore, whilst sharing a high spatial overlap with the ground truth, inferred CNN-based segmentations can lack coherence, including spurious connected components, holes and voids. Such results are implausible, violating anticipated anatomical topology. In response, (single-class) persistent homology-based loss functions have been proposed to capture global anatomical features. Our work extends these approaches to the task of multi-class segmentation. Building an enriched topological description of all class labels and class label pairs, our loss functions make predictable and statistically significant improvements in segmentation topology using a CNN-based post-processing framework. We also present (and make available) a highly efficient implementation based on cubical complexes and parallel execution, enabling practical application within high resolution 3D data for the first time. We demonstrate our approach on 2D short axis and 3D whole heart CMR segmentation, advancing a detailed and faithful analysis of performance on two publicly available datasets.

Active Training of Physics-Informed Neural Networks to Aggregate and Interpolate Parametric Solutions to the Navier-Stokes Equations

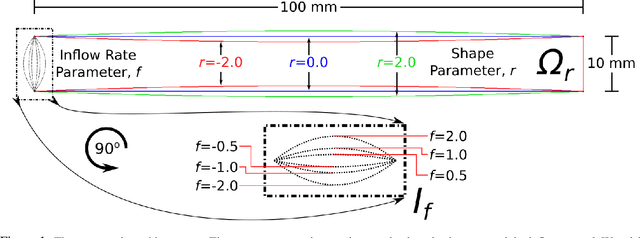
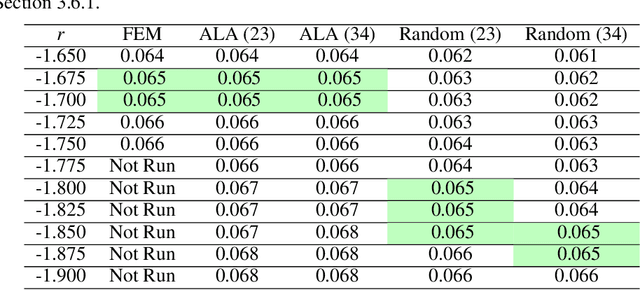
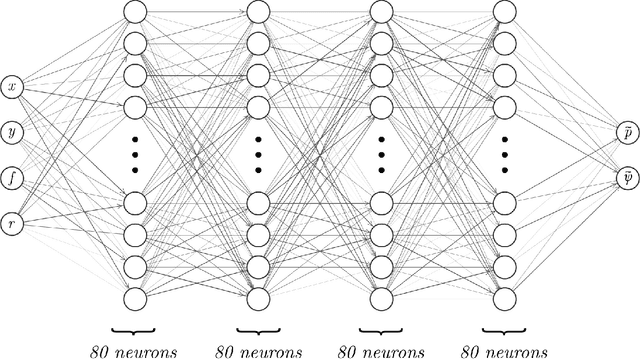
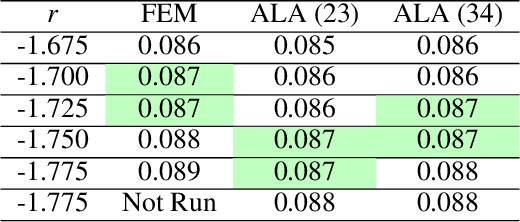
The goal of this work is to train a neural network which approximates solutions to the Navier-Stokes equations across a region of parameter space, in which the parameters define physical properties such as domain shape and boundary conditions. The contributions of this work are threefold: 1) To demonstrate that neural networks can be efficient aggregators of whole families of parameteric solutions to physical problems, trained using data created with traditional, trusted numerical methods such as finite elements. Advantages include extremely fast evaluation of pressure and velocity at any point in physical and parameter space (asymptotically, ~3 $\mu s$ / query), and data compression (the network requires 99\% less storage space compared to its own training data). 2) To demonstrate that the neural networks can accurately interpolate between finite element solutions in parameter space, allowing them to be instantly queried for pressure and velocity field solutions to problems for which traditional simulations have never been performed. 3) To introduce an active learning algorithm, so that during training, a finite element solver can automatically be queried to obtain additional training data in locations where the neural network's predictions are in most need of improvement, thus autonomously acquiring and efficiently distributing training data throughout parameter space. In addition to the obvious utility of Item 2, above, we demonstrate an application of the network in rapid parameter sweeping, very precisely predicting the degree of narrowing in a tube which would result in a 50\% increase in end-to-end pressure difference at a given flow rate. This capability could have applications in both medical diagnosis of arterial disease, and in computer-aided design.