VNT-Net: Rotational Invariant Vector Neuron Transformers

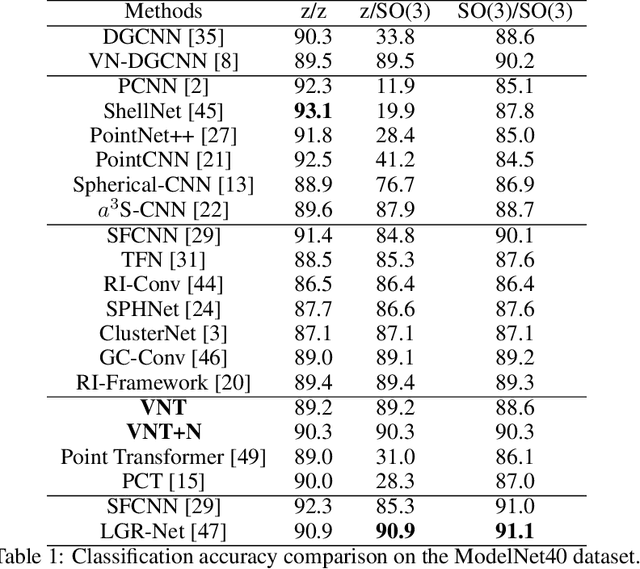
Learning 3D point sets with rotational invariance is an important and challenging problem in machine learning. Through rotational invariant architectures, 3D point cloud neural networks are relieved from requiring a canonical global pose and from exhaustive data augmentation with all possible rotations. In this work, we introduce a rotational invariant neural network by combining recently introduced vector neurons with self-attention layers to build a point cloud vector neuron transformer network (VNT-Net). Vector neurons are known for their simplicity and versatility in representing SO(3) actions and are thereby incorporated in common neural operations. Similarly, Transformer architectures have gained popularity and recently were shown successful for images by applying directly on sequences of image patches and achieving superior performance and convergence. In order to benefit from both worlds, we combine the two structures by mainly showing how to adapt the multi-headed attention layers to comply with vector neurons operations. Through this adaptation attention layers become SO(3) and the overall network becomes rotational invariant. Experiments demonstrate that our network efficiently handles 3D point cloud objects in arbitrary poses. We also show that our network achieves higher accuracy when compared to related state-of-the-art methods and requires less training due to a smaller number of hyperparameters in common classification and segmentation tasks.

Multi-modal 3D Shape Reconstruction Under Calibration Uncertainty using Parametric Level Set Methods

We consider the problem of 3D shape reconstruction from multi-modal data, given uncertain calibration parameters. Typically, 3D data modalities can be in diverse forms such as sparse point sets, volumetric slices, 2D photos and so on. To jointly process these data modalities, we exploit a parametric level set method that utilizes ellipsoidal radial basis functions. This method not only allows us to analytically and compactly represent the object, it also confers on us the ability to overcome calibration related noise that originates from inaccurate acquisition parameters. This essentially implicit regularization leads to a highly robust and scalable reconstruction, surpassing other traditional methods. In our results we first demonstrate the ability of the method to compactly represent complex objects. We then show that our reconstruction method is robust both to a small number of measurements and to noise in the acquisition parameters. Finally, we demonstrate our reconstruction abilities from diverse modalities such as volume slices obtained from liquid displacement (similar to CTscans and XRays), and visual measurements obtained from shape silhouettes.

A Non-linear Differential CNN-Rendering Module for 3D Data Enhancement

In this work we introduce a differential rendering module which allows neural networks to efficiently process cluttered data. The module is composed of continuous piecewise differentiable functions defined as a sensor array of cells embedded in 3D space. Our module is learnable and can be easily integrated into neural networks allowing to optimize data rendering towards specific learning tasks using gradient based methods in an end-to-end fashion. Essentially, the module's sensor cells are allowed to transform independently and locally focus and sense different parts of the 3D data. Thus, through their optimization process, cells learn to focus on important parts of the data, bypassing occlusions, clutter and noise. Since sensor cells originally lie on a grid, this equals to a highly non-linear rendering of the scene into a 2D image. Our module performs especially well in presence of clutter and occlusions. Similarly, it deals well with non-linear deformations and improves classification accuracy through proper rendering of the data. In our experiments, we apply our module to demonstrate efficient localization and classification tasks in cluttered data both 2D and 3D.