Evaluation of Data Augmentation and Loss Functions in Semantic Image Segmentation for Drilling Tool Wear Detection

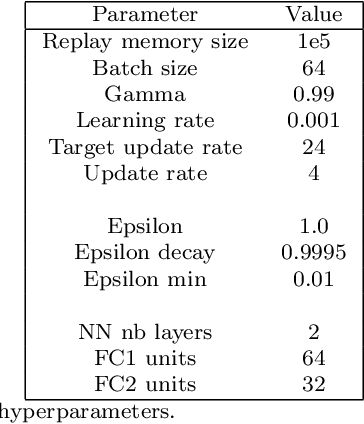
Tool wear monitoring is crucial for quality control and cost reduction in manufacturing processes, of which drilling applications are one example. In this paper, we present a U-Net based semantic image segmentation pipeline, deployed on microscopy images of cutting inserts, for the purpose of wear detection. The wear area is differentiated in two different types, resulting in a multiclass classification problem. Joining the two wear types in one general wear class, on the other hand, allows the problem to be formulated as a binary classification task. Apart from the comparison of the binary and multiclass problem, also different loss functions, i. e., Cross Entropy, Focal Cross Entropy, and a loss based on the Intersection over Union (IoU), are investigated. Furthermore, models are trained on image tiles of different sizes, and augmentation techniques of varying intensities are deployed. We find, that the best performing models are binary models, trained on data with moderate augmentation and an IoU-based loss function.

Automatic Detection of Interplanetary Coronal Mass Ejections in Solar Wind In Situ Data

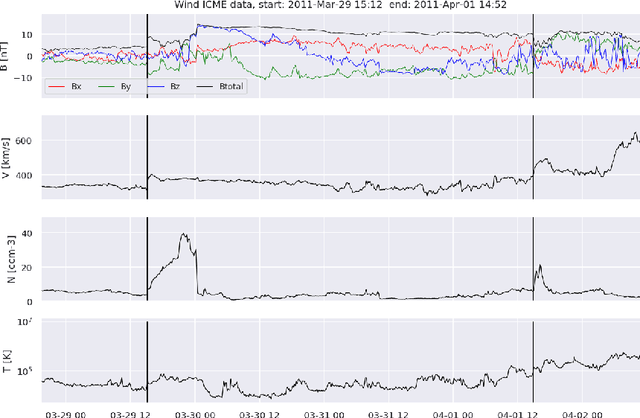
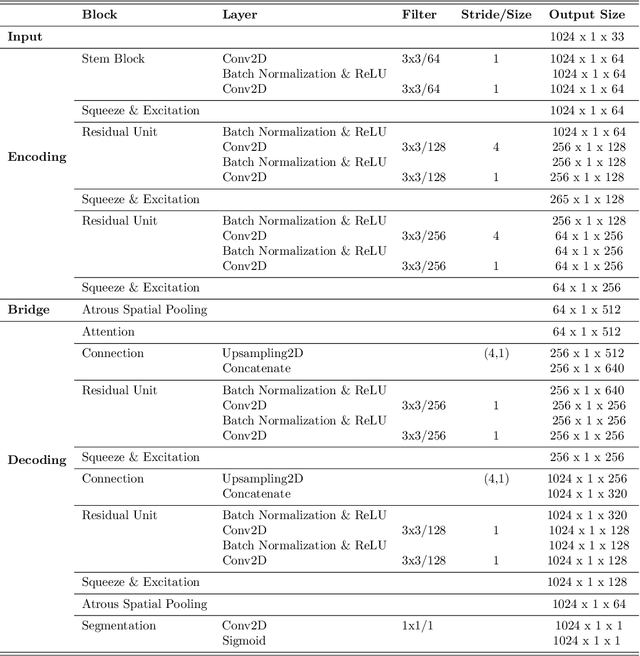
Interplanetary coronal mass ejections (ICMEs) are one of the main drivers for space weather disturbances. In the past, different approaches have been used to automatically detect events in existing time series resulting from solar wind in situ observations. However, accurate and fast detection still remains a challenge when facing the large amount of data from different instruments. For the automatic detection of ICMEs we propose a pipeline using a method that has recently proven successful in medical image segmentation. Comparing it to an existing method, we find that while achieving similar results, our model outperforms the baseline regarding training time by a factor of approximately 20, thus making it more applicable for other datasets. The method has been tested on in situ data from the Wind spacecraft between 1997 and 2015 with a True Skill Statistic (TSS) of 0.64. Out of the 640 ICMEs, 466 were detected correctly by our algorithm, producing a total of 254 False Positives. Additionally, it produced reasonable results on datasets with fewer features and smaller training sets from Wind, STEREO-A and STEREO-B with True Skill Statistics of 0.56, 0.57 and 0.53, respectively. Our pipeline manages to find the start of an ICME with a mean absolute error (MAE) of around 2 hours and 56 minutes, and the end time with a MAE of 3 hours and 20 minutes. The relatively fast training allows straightforward tuning of hyperparameters and could therefore easily be used to detect other structures and phenomena in solar wind data, such as corotating interaction regions.

Vehicle management in a modular production context using Deep Q-Learning

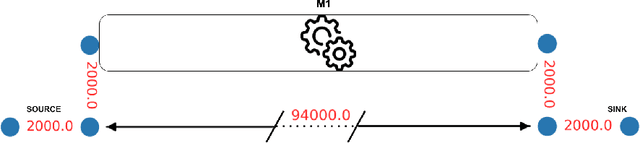
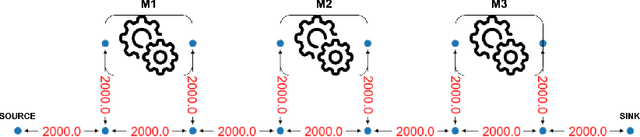
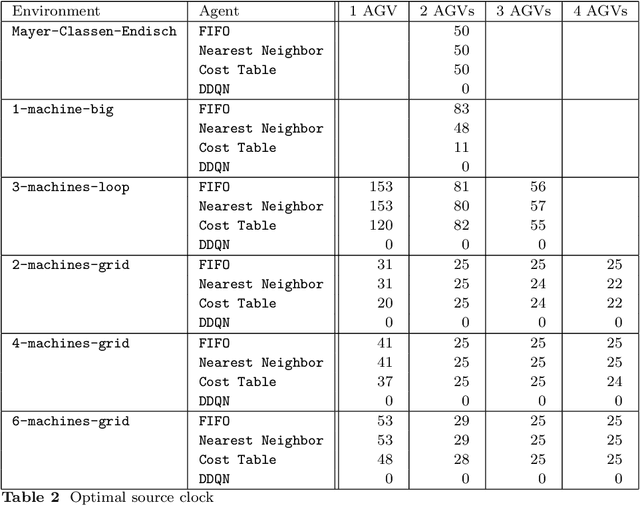
We investigate the feasibility of deploying Deep-Q based deep reinforcement learning agents to job-shop scheduling problems in the context of modular production facilities, using discrete event simulations for the environment. These environments are comprised of a source and sink for the parts to be processed, as well as (several) workstations. The agents are trained to schedule automated guided vehicles to transport the parts back and forth between those stations in an optimal fashion. Starting from a very simplistic setup, we increase the complexity of the environment and compare the agents' performances with well established heuristic approaches, such as first-in-first-out based agents, cost tables and a nearest-neighbor approach. We furthermore seek particular configurations of the environments in which the heuristic approaches struggle, to investigate to what degree the Deep-Q agents are affected by these challenges. We find that Deep-Q based agents show comparable performance as the heuristic baselines. Furthermore, our findings suggest that the DRL agents exhibit an increased robustness to noise, as compared to the conventional approaches. Overall, we find that DRL agents constitute a valuable approach for this type of scheduling problems.

A machine learning pipeline for autonomous numerical analytic continuation of Dyson-Schwinger equations

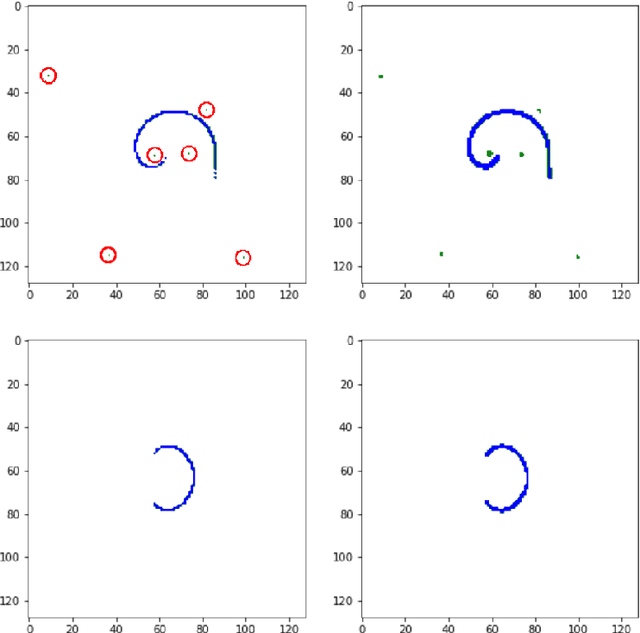
Dyson-Schwinger equations (DSEs) are a non-perturbative way to express n-point functions in quantum field theory. Working in Euclidean space and in Landau gauge, for example, one can study the quark propagator Dyson-Schwinger equation in the real and complex domain, given that a suitable and tractable truncation has been found. When aiming for solving these equations in the complex domain, that is, for complex external momenta, one has to deform the integration contour of the radial component in the complex plane of the loop momentum expressed in hyper-spherical coordinates. This has to be done in order to avoid poles and branch cuts in the integrand of the self-energy loop. Since the nature of Dyson-Schwinger equations is such, that they have to be solved in a self-consistent way, one cannot analyze the analytic properties of the integrand after every iteration step, as this would not be feasible. In these proceedings, we suggest a machine learning pipeline based on deep learning (DL) approaches to computer vision (CV), as well as deep reinforcement learning (DRL), that could solve this problem autonomously by detecting poles and branch cuts in the numerical integrand after every iteration step and by suggesting suitable integration contour deformations that avoid these obstructions. We sketch out a proof of principle for both of these tasks, that is, the pole and branch cut detection, as well as the contour deformation.

Deep reinforcement learning for complex evaluation of one-loop diagrams in quantum field theory

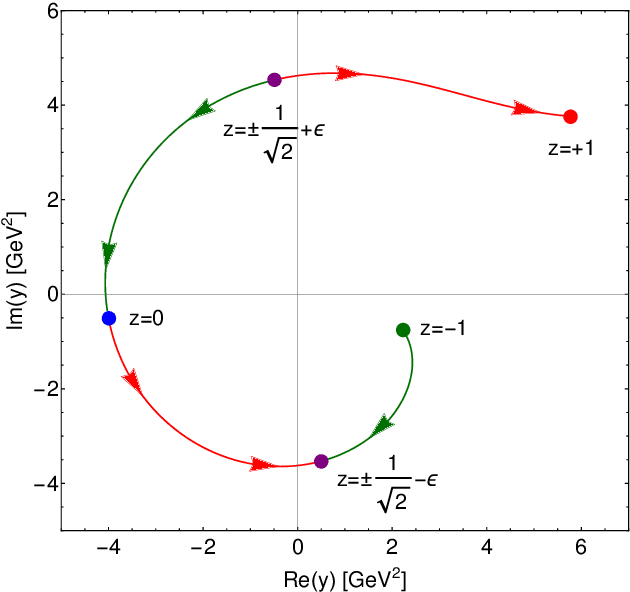
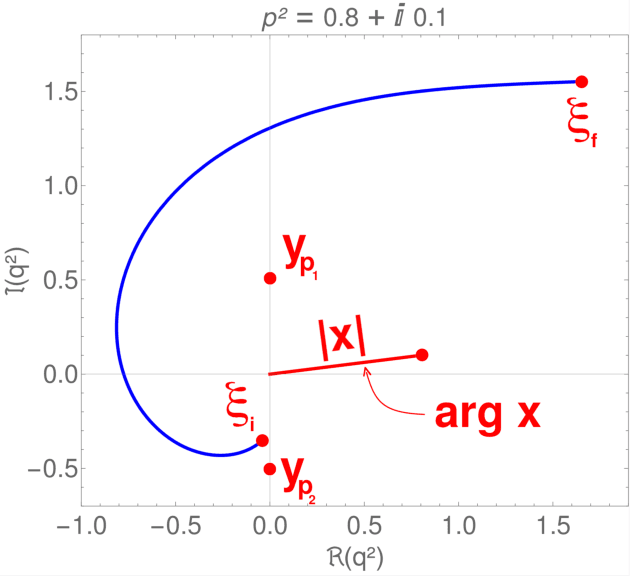
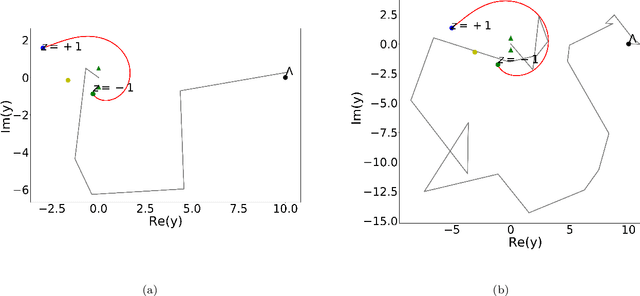
In this paper we present a novel technique based on deep reinforcement learning that allows for numerical analytic continuation of integrals that are often encountered in one-loop diagrams in quantum field theory. In order to extract certain quantities of two-point functions, such as spectral densities, mass poles or multi-particle thresholds, it is necessary to perform an analytic continuation of the correlator in question. At one-loop level in Euclidean space, this results in the necessity to deform the integration contour of the loop integral in the complex plane of the square of the loop momentum, in order to avoid non-analyticities in the integration plane. Using a toy model for which an exact solution is known, we train a reinforcement learning agent to perform the required contour deformations. Our study shows great promise for an agent to be deployed in iterative numerical approaches used to compute non-perturbative 2-point functions, such as the quark propagator Dyson-Schwinger equation, or more generally, Fredholm equations of the second kind, in the complex domain.