Anomaly Detection in Complex Dynamical Systems: A Systematic Framework Using Embedding Theory and Physics-Inspired Consistency

Anomaly detection in complex dynamical systems is essential for ensuring reliability, safety, and efficiency in industrial and cyber-physical infrastructures. Predictive maintenance helps prevent costly failures, while cybersecurity monitoring has become critical as digitized systems face growing threats. Many of these systems exhibit oscillatory behaviors and bounded motion, requiring anomaly detection methods that capture structured temporal dependencies while adhering to physical consistency principles. In this work, we propose a system-theoretic approach to anomaly detection, grounded in classical embedding theory and physics-inspired consistency principles. We build upon the Fractal Whitney Embedding Prevalence Theorem, extending traditional embedding techniques to complex system dynamics. Additionally, we introduce state-derivative pairs as an embedding strategy to capture system evolution. To enforce temporal coherence, we develop a Temporal Differential Consistency Autoencoder (TDC-AE), incorporating a TDC-Loss that aligns the approximated derivatives of latent variables with their dynamic representations. We evaluate our method on the C-MAPSS dataset, a benchmark for turbofan aeroengine degradation. TDC-AE outperforms LSTMs and Transformers while achieving a 200x reduction in MAC operations, making it particularly suited for lightweight edge computing. Our findings support the hypothesis that anomalies disrupt stable system dynamics, providing a robust, interpretable signal for anomaly detection.

A machine learning pipeline for autonomous numerical analytic continuation of Dyson-Schwinger equations

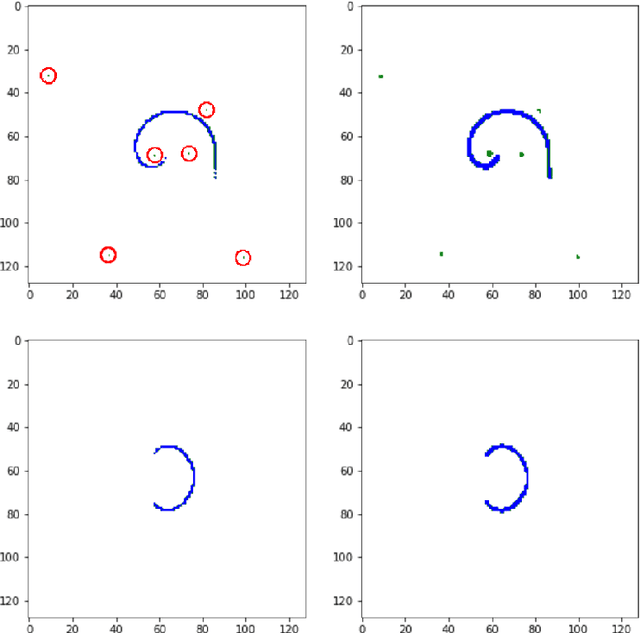
Dyson-Schwinger equations (DSEs) are a non-perturbative way to express n-point functions in quantum field theory. Working in Euclidean space and in Landau gauge, for example, one can study the quark propagator Dyson-Schwinger equation in the real and complex domain, given that a suitable and tractable truncation has been found. When aiming for solving these equations in the complex domain, that is, for complex external momenta, one has to deform the integration contour of the radial component in the complex plane of the loop momentum expressed in hyper-spherical coordinates. This has to be done in order to avoid poles and branch cuts in the integrand of the self-energy loop. Since the nature of Dyson-Schwinger equations is such, that they have to be solved in a self-consistent way, one cannot analyze the analytic properties of the integrand after every iteration step, as this would not be feasible. In these proceedings, we suggest a machine learning pipeline based on deep learning (DL) approaches to computer vision (CV), as well as deep reinforcement learning (DRL), that could solve this problem autonomously by detecting poles and branch cuts in the numerical integrand after every iteration step and by suggesting suitable integration contour deformations that avoid these obstructions. We sketch out a proof of principle for both of these tasks, that is, the pole and branch cut detection, as well as the contour deformation.

Deep reinforcement learning for complex evaluation of one-loop diagrams in quantum field theory

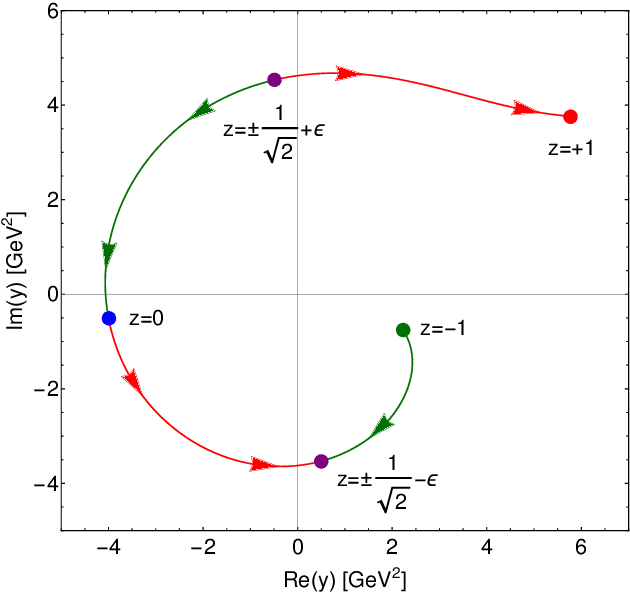
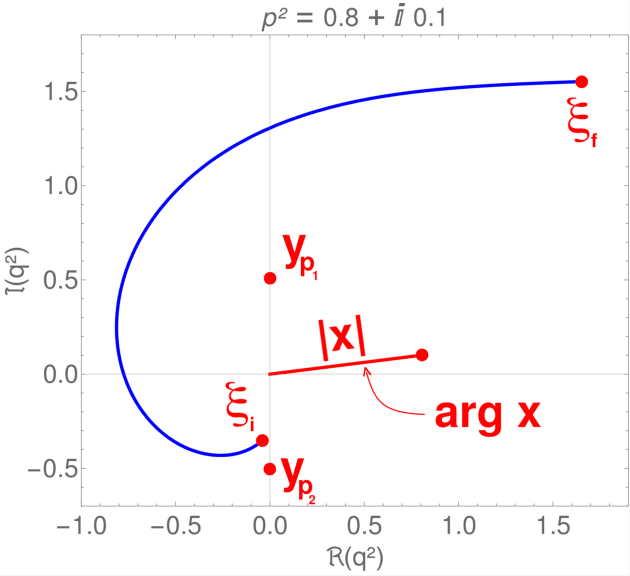
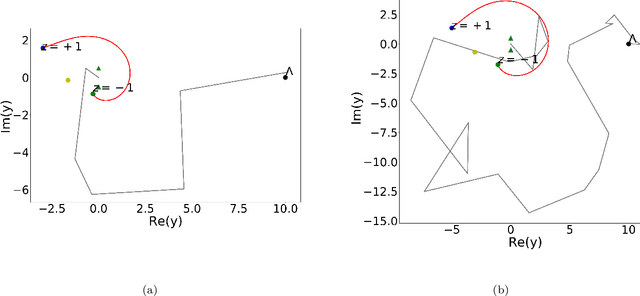
In this paper we present a novel technique based on deep reinforcement learning that allows for numerical analytic continuation of integrals that are often encountered in one-loop diagrams in quantum field theory. In order to extract certain quantities of two-point functions, such as spectral densities, mass poles or multi-particle thresholds, it is necessary to perform an analytic continuation of the correlator in question. At one-loop level in Euclidean space, this results in the necessity to deform the integration contour of the loop integral in the complex plane of the square of the loop momentum, in order to avoid non-analyticities in the integration plane. Using a toy model for which an exact solution is known, we train a reinforcement learning agent to perform the required contour deformations. Our study shows great promise for an agent to be deployed in iterative numerical approaches used to compute non-perturbative 2-point functions, such as the quark propagator Dyson-Schwinger equation, or more generally, Fredholm equations of the second kind, in the complex domain.