Andreas Heuer
Critical nonlinear aspects of hopping transport for reconfigurable logic in disordered dopant networks
Dec 26, 2023Abstract:Nonlinear behavior in the hopping transport of interacting charges enables reconfigurable logic in disordered dopant network devices, where voltages applied at control electrodes tune the relation between voltages applied at input electrodes and the current measured at an output electrode. From kinetic Monte Carlo simulations we analyze the critical nonlinear aspects of variable-range hopping transport for realizing Boolean logic gates in these devices on three levels. First, we quantify the occurrence of individual gates for random choices of control voltages. We find that linearly inseparable gates such as the XOR gate are less likely to occur than linearly separable gates such as the AND gate, despite the fact that the number of different regions in the multidimensional control voltage space for which AND or XOR gates occur is comparable. Second, we use principal component analysis to characterize the distribution of the output current vectors for the (00,10,01,11) logic input combinations in terms of eigenvectors and eigenvalues of the output covariance matrix. This allows a simple and direct comparison of the behavior of different simulated devices and a comparison to experimental devices. Third, we quantify the nonlinearity in the distribution of the output current vectors necessary for realizing Boolean functionality by introducing three nonlinearity indicators. The analysis provides a physical interpretation of the effects of changing the hopping distance and temperature and is used in a comparison with data generated by a deep neural network trained on a physical device.
A kinetic Monte Carlo Approach for Boolean Logic Functionality in Gold Nanoparticle Networks
Dec 07, 2023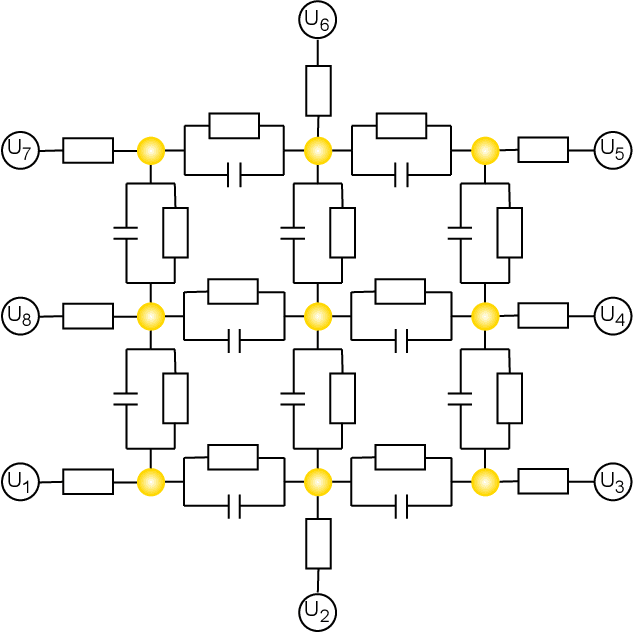
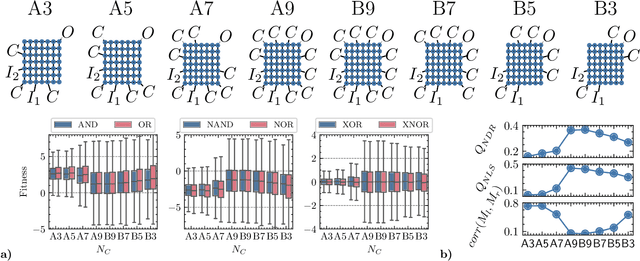
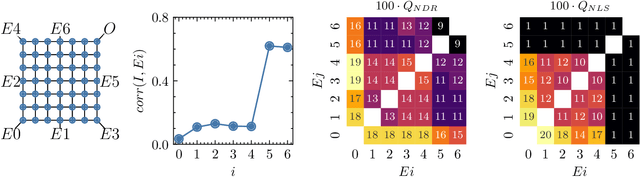
Abstract:Nanoparticles interconnected by insulating organic molecules exhibit nonlinear switching behavior at low temperatures. By assembling these switches into a network and manipulating charge transport dynamics through surrounding electrodes, the network can be reconfigurably functionalized to act as any Boolean logic gate. This work introduces a kinetic Monte Carlo-based simulation tool, applying established principles of single electronics to model charge transport dynamics in nanoparticle networks. We functionalize nanoparticle networks as Boolean logic gates and assess their quality using a fitness function. Based on the definition of fitness, we derive new metrics to quantify essential nonlinear properties of the network, including negative differential resistance and nonlinear separability. These nonlinear properties are crucial not only for functionalizing the network as Boolean logic gates but also when our networks are functionalized for brain-inspired computing applications in the future. We address fundamental questions about the dependence of fitness and nonlinear properties on system size, number of surrounding electrodes, and electrode positioning. We assert the overall benefit of having more electrodes, with proximity to the network's output being pivotal for functionality and nonlinearity. Additionally, we demonstrate a optimal system size and argue for breaking symmetry in electrode positioning to favor nonlinear properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge