CoordGate: Efficiently Computing Spatially-Varying Convolutions in Convolutional Neural Networks

Optical imaging systems are inherently limited in their resolution due to the point spread function (PSF), which applies a static, yet spatially-varying, convolution to the image. This degradation can be addressed via Convolutional Neural Networks (CNNs), particularly through deblurring techniques. However, current solutions face certain limitations in efficiently computing spatially-varying convolutions. In this paper we propose CoordGate, a novel lightweight module that uses a multiplicative gate and a coordinate encoding network to enable efficient computation of spatially-varying convolutions in CNNs. CoordGate allows for selective amplification or attenuation of filters based on their spatial position, effectively acting like a locally connected neural network. The effectiveness of the CoordGate solution is demonstrated within the context of U-Nets and applied to the challenging problem of image deblurring. The experimental results show that CoordGate outperforms conventional approaches, offering a more robust and spatially aware solution for CNNs in various computer vision applications.

Data-driven Science and Machine Learning Methods in Laser-Plasma Physics

Laser-plasma physics has developed rapidly over the past few decades as lasers have become both more powerful and more widely available. Early experimental and numerical research in this field was dominated by single-shot experiments with limited parameter exploration. However, recent technological improvements make it possible to gather data for hundreds or thousands of different settings in both experiments and simulations. This has sparked interest in using advanced techniques from mathematics, statistics and computer science to deal with, and benefit from, big data. At the same time, sophisticated modeling techniques also provide new ways for researchers to deal effectively with situation where still only sparse data are available. This paper aims to present an overview of relevant machine learning methods with focus on applicability to laser-plasma physics and its important sub-fields of laser-plasma acceleration and inertial confinement fusion.

Multi-objective and multi-fidelity Bayesian optimization of laser-plasma acceleration

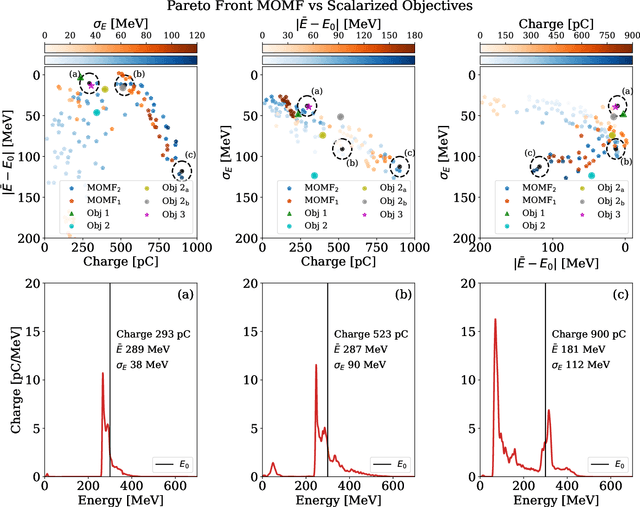
Beam parameter optimization in accelerators involves multiple, sometimes competing objectives. Condensing these multiple objectives into a single objective unavoidably results in bias towards particular outcomes that do not necessarily represent the best possible outcome for the operator in terms of parameter optimization. A more versatile approach is multi-objective optimization, which establishes the trade-off curve or Pareto front between objectives. Here we present first results on multi-objective Bayesian optimization of a simulated laser-plasma accelerator. We find that multi-objective optimization is equal or even superior in performance to its single-objective counterparts, and that it is more resilient to different statistical descriptions of objectives. As a second major result of our paper, we significantly reduce the computational costs of the optimization by choosing the resolution and box size of the simulations dynamically. This is relevant since even with the use of Bayesian statistics, performing such optimizations on a multi-dimensional search space may require hundreds or thousands of simulations. Our algorithm translates information gained from fast, low-resolution runs with lower fidelity to high-resolution data, thus requiring fewer actual simulations at highest computational cost. The techniques demonstrated in this paper can be translated to many different use cases, both computational and experimental.

Expected hypervolume improvement for simultaneous multi-objective and multi-fidelity optimization

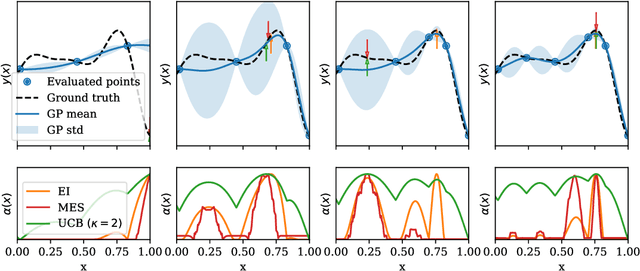
Bayesian optimization has proven to be an efficient method to optimize expensive-to-evaluate systems. However, depending on the cost of single observations, multi-dimensional optimizations of one or more objectives may still be prohibitively expensive. Multi-fidelity optimization remedies this issue by including multiple, cheaper information sources such as low-resolution approximations in numerical simulations. Acquisition functions for multi-fidelity optimization are typically based on exploration-heavy algorithms that are difficult to combine with optimization towards multiple objectives. Here we show that the expected hypervolume improvement policy can act in many situations as a suitable substitute. We incorporate the evaluation cost either via a two-step evaluation or within a single acquisition function with an additional fidelity-related objective. This permits simultaneous multi-objective and multi-fidelity optimization, which allows to accurately establish the Pareto set and front at fractional cost. Benchmarks show a cost reduction of an order of magnitude or more. Our method thus allows for Pareto optimization of extremely expansive black-box functions. The presented methods are simple and straightforward to implement in existing, optimized Bayesian optimization frameworks and can immediately be extended to batch optimization. The techniques can also be used to combine different continuous and/or discrete fidelity dimensions, which makes them particularly relevant for simulation problems in plasma physics, fluid dynamics and many other branches of scientific computing.