Multi-objective and multi-fidelity Bayesian optimization of laser-plasma acceleration

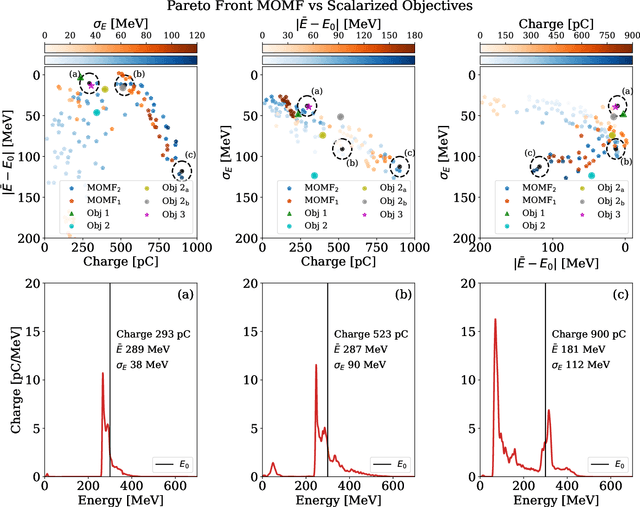
Beam parameter optimization in accelerators involves multiple, sometimes competing objectives. Condensing these multiple objectives into a single objective unavoidably results in bias towards particular outcomes that do not necessarily represent the best possible outcome for the operator in terms of parameter optimization. A more versatile approach is multi-objective optimization, which establishes the trade-off curve or Pareto front between objectives. Here we present first results on multi-objective Bayesian optimization of a simulated laser-plasma accelerator. We find that multi-objective optimization is equal or even superior in performance to its single-objective counterparts, and that it is more resilient to different statistical descriptions of objectives. As a second major result of our paper, we significantly reduce the computational costs of the optimization by choosing the resolution and box size of the simulations dynamically. This is relevant since even with the use of Bayesian statistics, performing such optimizations on a multi-dimensional search space may require hundreds or thousands of simulations. Our algorithm translates information gained from fast, low-resolution runs with lower fidelity to high-resolution data, thus requiring fewer actual simulations at highest computational cost. The techniques demonstrated in this paper can be translated to many different use cases, both computational and experimental.