SAGA: Score-Weighted Adaptive Generation Alignment for Low-Resource Nordic Language Models

Preference optimisation has proven effective for improving large language models but typically relies on costly human preference annotations. Extending these methods to morphologically rich, low-resource languages remains challenging because such annotations are scarce. We present SAGA (Score-weighted Adaptive Generation Alignment), a parser-guided preference optimisation framework that replaces human labels with dependency-parser supervision. SAGA converts parser judgements into preference pairs for delta-DPO, combines parser quality with lexical diversity in a composite reward, filters low-information pairs using a reward-gap criterion, and monitors reward hacking to maintain reliable supervision. Across Danish, Icelandic, and Norwegian Bokmål using GPT-SW3-1.3B, SAGA consistently improves grammatical quality without requiring human preference labels. Danish parse success increases from 69.0% to 93.8%, Icelandic achieves a +4.5 percentage-point improvement on an independent Stanza evaluation (three-run mean +3.3 percentage points) while native speakers prefer SAGA outputs in 80% of pairwise comparisons, and Norwegian Bokmål improves by +28 percentage points. These results demonstrate that parser-derived supervision is a practical alternative to human preference annotation for grammatical alignment in low-resource languages where high-quality dependency parsers are available.

Deep Inductive Logic Programming meets Reinforcement Learning

One approach to explaining the hierarchical levels of understanding within a machine learning model is the symbolic method of inductive logic programming (ILP), which is data efficient and capable of learning first-order logic rules that can entail data behaviour. A differentiable extension to ILP, so-called differentiable Neural Logic (dNL) networks, are able to learn Boolean functions as their neural architecture includes symbolic reasoning. We propose an application of dNL in the field of Relational Reinforcement Learning (RRL) to address dynamic continuous environments. This represents an extension of previous work in applying dNL-based ILP in RRL settings, as our proposed model updates the architecture to enable it to solve problems in continuous RL environments. The goal of this research is to improve upon current ILP methods for use in RRL by incorporating non-linear continuous predicates, allowing RRL agents to reason and make decisions in dynamic and continuous environments.

Explainability in Machine Learning: a Pedagogical Perspective

Given the importance of integrating of explainability into machine learning, at present, there are a lack of pedagogical resources exploring this. Specifically, we have found a need for resources in explaining how one can teach the advantages of explainability in machine learning. Often pedagogical approaches in the field of machine learning focus on getting students prepared to apply various models in the real world setting, but much less attention is given to teaching students the various techniques one could employ to explain a model's decision-making process. Furthermore, explainability can benefit from a narrative structure that aids one in understanding which techniques are governed by which questions about the data. We provide a pedagogical perspective on how to structure the learning process to better impart knowledge to students and researchers in machine learning, when and how to implement various explainability techniques as well as how to interpret the results. We discuss a system of teaching explainability in machine learning, by exploring the advantages and disadvantages of various opaque and transparent machine learning models, as well as when to utilize specific explainability techniques and the various frameworks used to structure the tools for explainability. Among discussing concrete assignments, we will also discuss ways to structure potential assignments to best help students learn to use explainability as a tool alongside any given machine learning application. Data science professionals completing the course will have a birds-eye view of a rapidly developing area and will be confident to deploy machine learning more widely. A preliminary analysis on the effectiveness of a recently delivered course following the structure presented here is included as evidence supporting our pedagogical approach.

Tractable Querying and Learning in Hybrid Domains via Sum-Product Networks

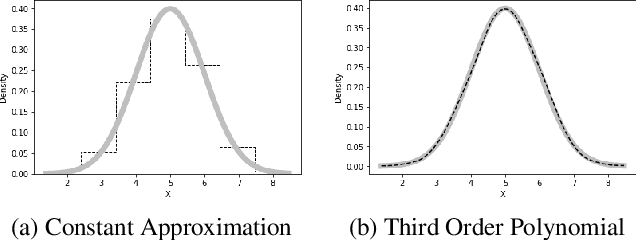
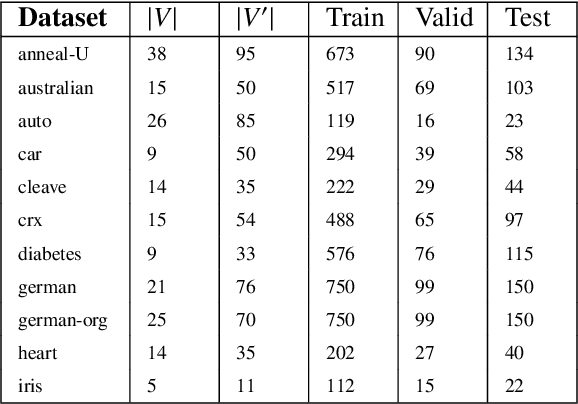
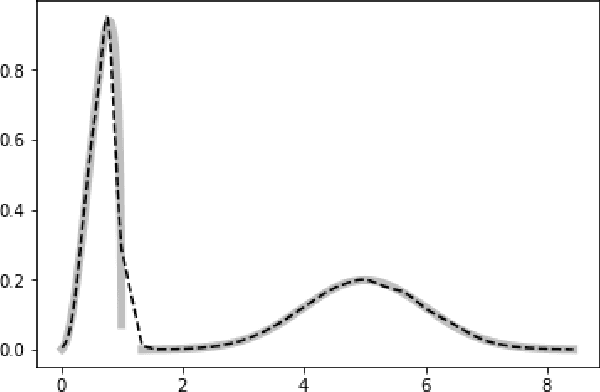
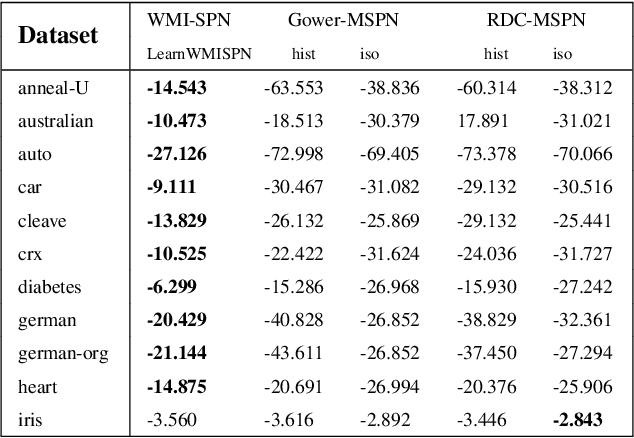
Probabilistic representations, such as Bayesian and Markov networks, are fundamental to much of statistical machine learning. Thus, learning probabilistic representations directly from data is a deep challenge, the main computational bottleneck being inference that is intractable. Tractable learning is a powerful new paradigm that attempts to learn distributions that support efficient probabilistic querying. By leveraging local structure, representations such as sum-product networks (SPNs) can capture high tree-width models with many hidden layers, essentially a deep architecture, while still admitting a range of probabilistic queries to be computable in time polynomial in the network size. The leaf nodes in SPNs, from which more intricate mixtures are formed, are tractable univariate distributions, and so the literature has focused on Bernoulli and Gaussian random variables. This is clearly a restriction for handling mixed discrete-continuous data, especially if the continuous features are generated from non-parametric and non-Gaussian distribution families. In this work, we present a framework that systematically integrates SPN structure learning with weighted model integration, a recently introduced computational abstraction for performing inference in hybrid domains, by means of piecewise polynomial approximations of density functions of arbitrary shape. Our framework is instantiated by exploiting the notion of propositional abstractions, thus minimally interfering with the SPN structure learning module, and supports a powerful query interface for conditioning on interval constraints. Our empirical results show that our approach is effective, and allows a study of the trade off between the granularity of the learned model and its predictive power.