Tractable Querying and Learning in Hybrid Domains via Sum-Product Networks

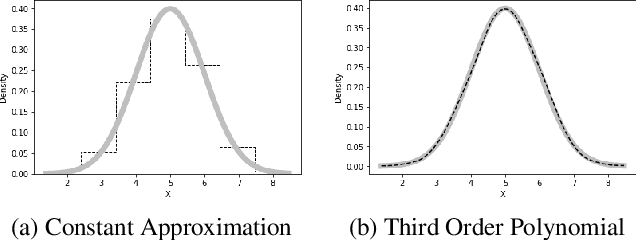
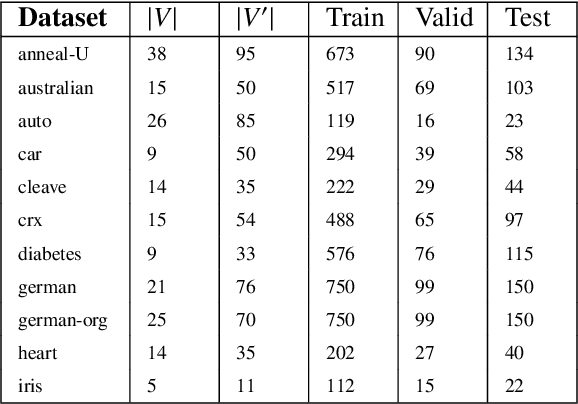
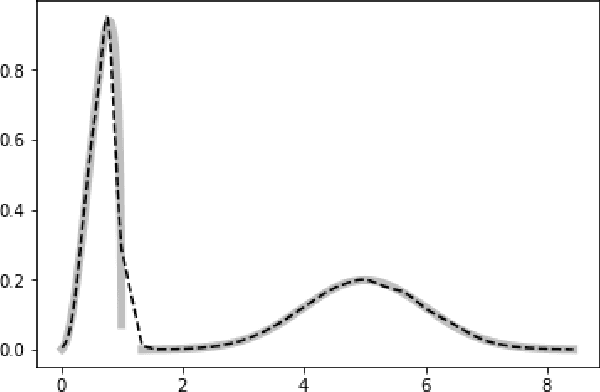
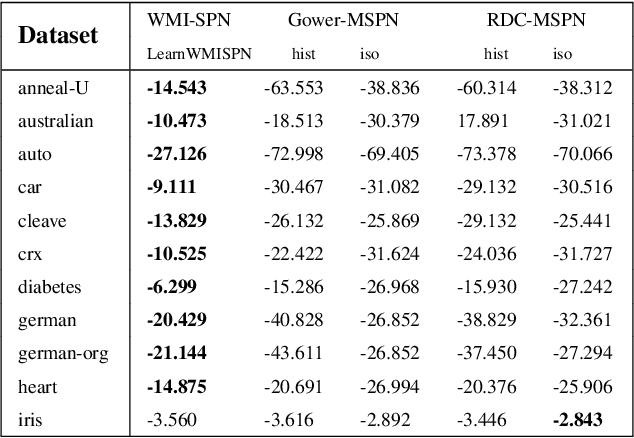
Probabilistic representations, such as Bayesian and Markov networks, are fundamental to much of statistical machine learning. Thus, learning probabilistic representations directly from data is a deep challenge, the main computational bottleneck being inference that is intractable. Tractable learning is a powerful new paradigm that attempts to learn distributions that support efficient probabilistic querying. By leveraging local structure, representations such as sum-product networks (SPNs) can capture high tree-width models with many hidden layers, essentially a deep architecture, while still admitting a range of probabilistic queries to be computable in time polynomial in the network size. The leaf nodes in SPNs, from which more intricate mixtures are formed, are tractable univariate distributions, and so the literature has focused on Bernoulli and Gaussian random variables. This is clearly a restriction for handling mixed discrete-continuous data, especially if the continuous features are generated from non-parametric and non-Gaussian distribution families. In this work, we present a framework that systematically integrates SPN structure learning with weighted model integration, a recently introduced computational abstraction for performing inference in hybrid domains, by means of piecewise polynomial approximations of density functions of arbitrary shape. Our framework is instantiated by exploiting the notion of propositional abstractions, thus minimally interfering with the SPN structure learning module, and supports a powerful query interface for conditioning on interval constraints. Our empirical results show that our approach is effective, and allows a study of the trade off between the granularity of the learned model and its predictive power.