Efficient Information Diffusion in Time-Varying Graphs through Deep Reinforcement Learning

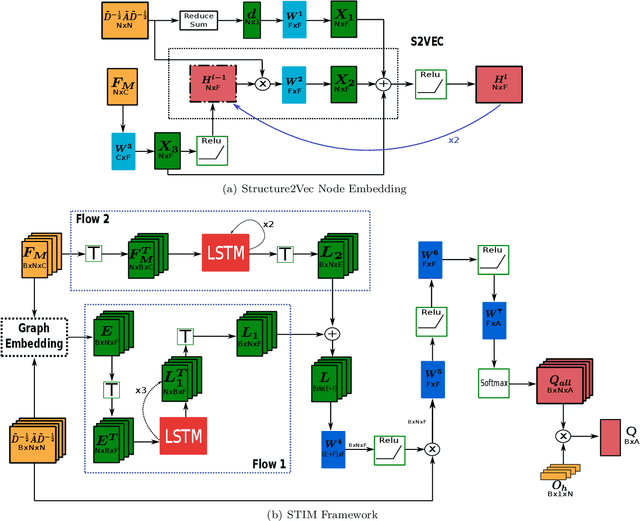
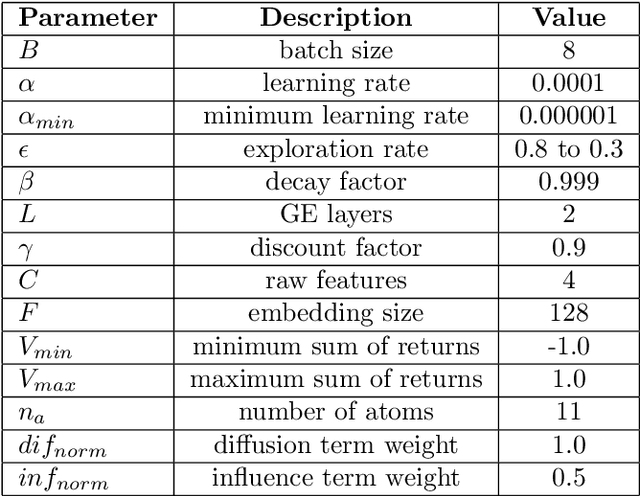
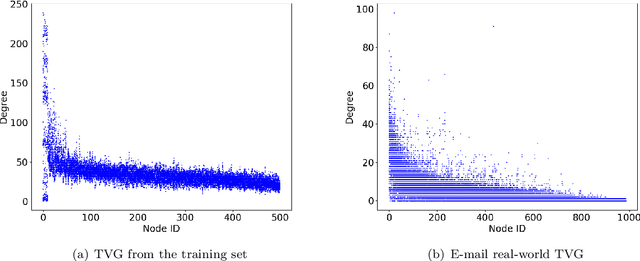
Network seeding for efficient information diffusion over time-varying graphs~(TVGs) is a challenging task with many real-world applications. There are several ways to model this spatio-temporal influence maximization problem, but the ultimate goal is to determine the best moment for a node to start the diffusion process. In this context, we propose Spatio-Temporal Influence Maximization~(STIM), a model trained with Reinforcement Learning and Graph Embedding over a set of artificial TVGs that is capable of learning the temporal behavior and connectivity pattern of each node, allowing it to predict the best moment to start a diffusion through the TVG. We also develop a special set of artificial TVGs used for training that simulate a stochastic diffusion process in TVGs, showing that the STIM network can learn an efficient policy even over a non-deterministic environment. STIM is also evaluated with a real-world TVG, where it also manages to efficiently propagate information through the nodes. Finally, we also show that the STIM model has a time complexity of $O(|E|)$. STIM, therefore, presents a novel approach for efficient information diffusion in TVGs, being highly versatile, where one can change the goal of the model by simply changing the adopted reward function.

Approximating Network Centrality Measures Using Node Embedding and Machine Learning

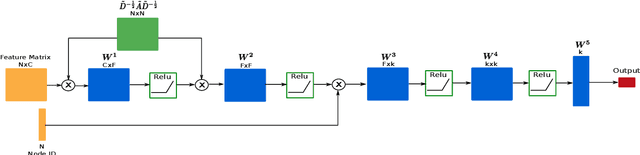
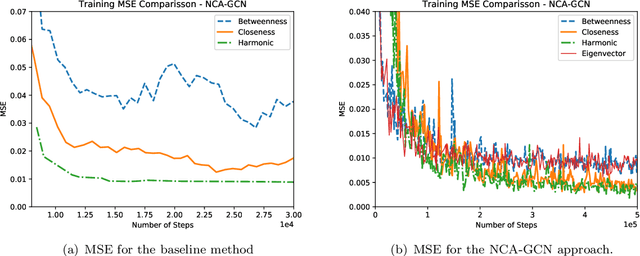
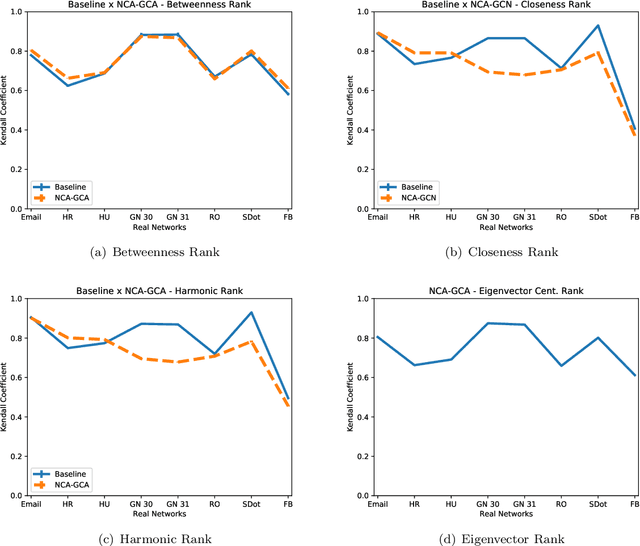
Analyzing and extracting useful information from real-world complex networks has become a key challenge due to the their large sizes such networks achieve nowadays. For instance, depending on the intended node centrality, it becomes unfeasible to compute it for such large complex networks due to the high computational cost. One way to tackle this problem is by developing fast methods capable of approximating the network centralities. In this paper, we propose an approach capable of efficiently approximating node centralities for large networks using Neural Networks and Node Embedding echniques. We thus call our approach the Network Centrality Approximation using Graph Convolutional Networks (NCA-GCN) model.In contrast to recent related work, the NCA-GCN model requires only the degree centrality of each node in order to predict any other centrality. We show that the NCA-GCN model works well in different node centralities for different network sizes.

Practical Kernel-Based Reinforcement Learning

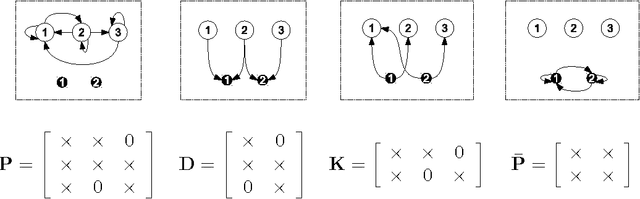
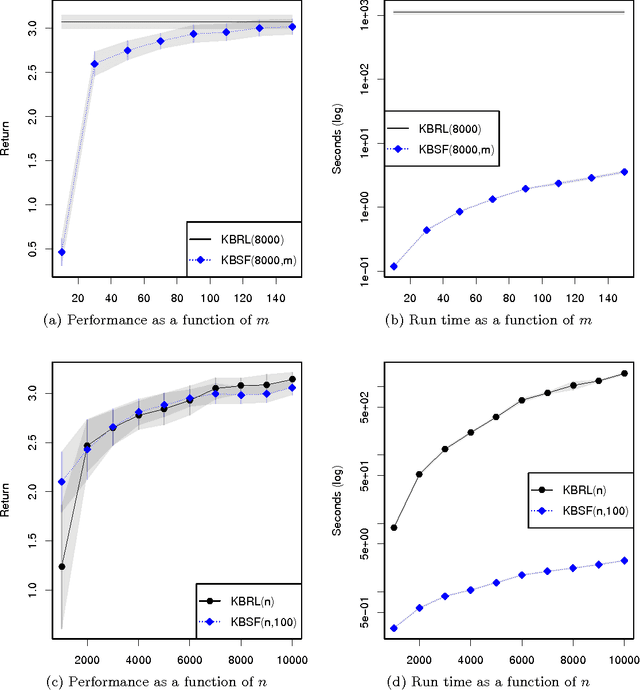
Kernel-based reinforcement learning (KBRL) stands out among reinforcement learning algorithms for its strong theoretical guarantees. By casting the learning problem as a local kernel approximation, KBRL provides a way of computing a decision policy which is statistically consistent and converges to a unique solution. Unfortunately, the model constructed by KBRL grows with the number of sample transitions, resulting in a computational cost that precludes its application to large-scale or on-line domains. In this paper we introduce an algorithm that turns KBRL into a practical reinforcement learning tool. Kernel-based stochastic factorization (KBSF) builds on a simple idea: when a transition matrix is represented as the product of two stochastic matrices, one can swap the factors of the multiplication to obtain another transition matrix, potentially much smaller, which retains some fundamental properties of its precursor. KBSF exploits such an insight to compress the information contained in KBRL's model into an approximator of fixed size. This makes it possible to build an approximation that takes into account both the difficulty of the problem and the associated computational cost. KBSF's computational complexity is linear in the number of sample transitions, which is the best one can do without discarding data. Moreover, the algorithm's simple mechanics allow for a fully incremental implementation that makes the amount of memory used independent of the number of sample transitions. The result is a kernel-based reinforcement learning algorithm that can be applied to large-scale problems in both off-line and on-line regimes. We derive upper bounds for the distance between the value functions computed by KBRL and KBSF using the same data. We also illustrate the potential of our algorithm in an extensive empirical study in which KBSF is applied to difficult tasks based on real-world data.

Classification-based Approximate Policy Iteration: Experiments and Extended Discussions

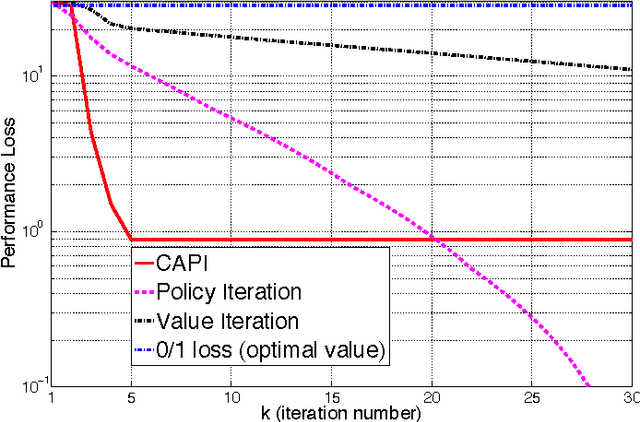
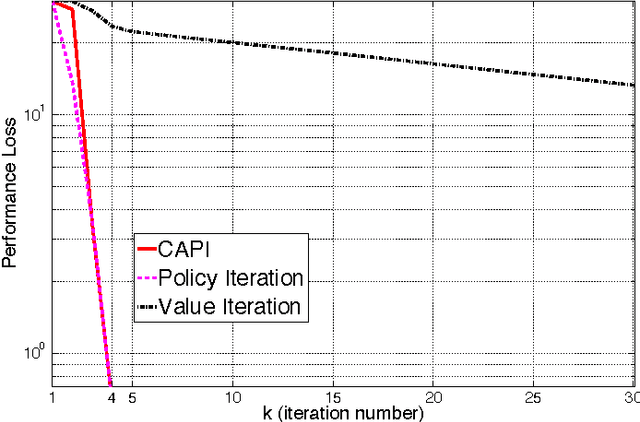
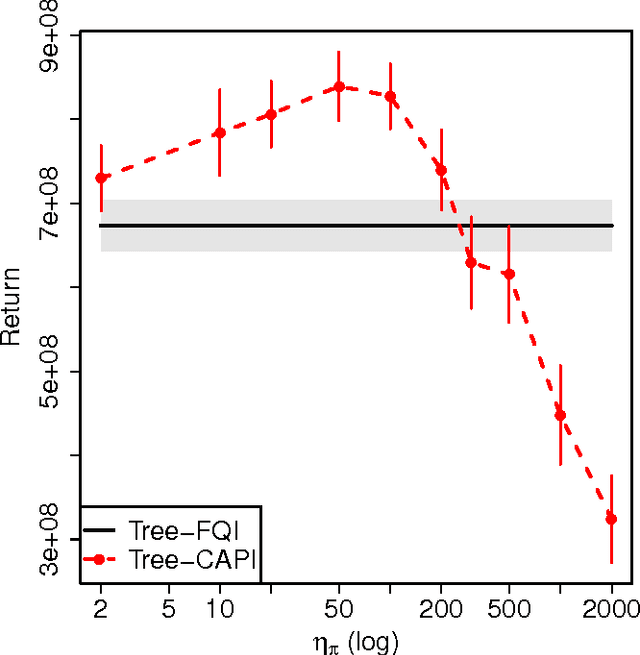
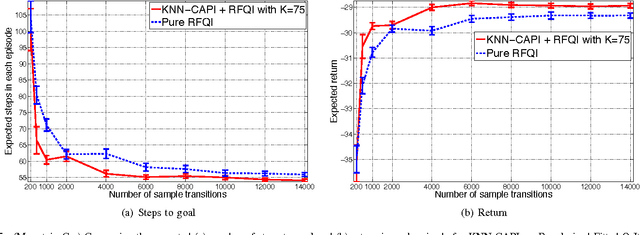
Tackling large approximate dynamic programming or reinforcement learning problems requires methods that can exploit regularities, or intrinsic structure, of the problem in hand. Most current methods are geared towards exploiting the regularities of either the value function or the policy. We introduce a general classification-based approximate policy iteration (CAPI) framework, which encompasses a large class of algorithms that can exploit regularities of both the value function and the policy space, depending on what is advantageous. This framework has two main components: a generic value function estimator and a classifier that learns a policy based on the estimated value function. We establish theoretical guarantees for the sample complexity of CAPI-style algorithms, which allow the policy evaluation step to be performed by a wide variety of algorithms (including temporal-difference-style methods), and can handle nonparametric representations of policies. Our bounds on the estimation error of the performance loss are tighter than existing results. We also illustrate this approach empirically on several problems, including a large HIV control task.