Quantile Surfaces -- Generalizing Quantile Regression to Multivariate Targets

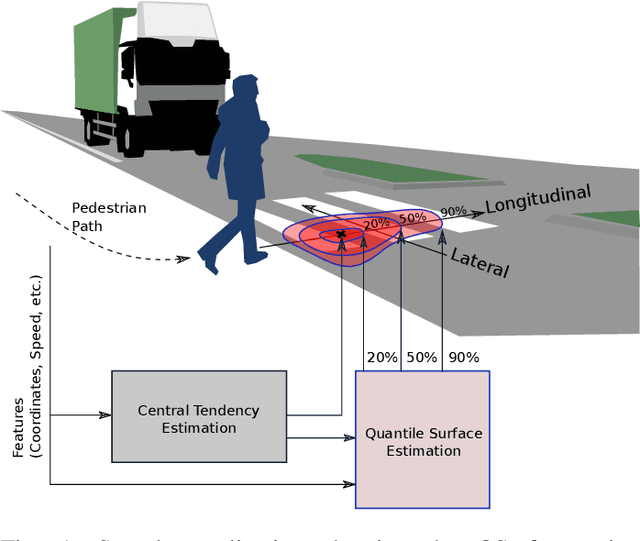
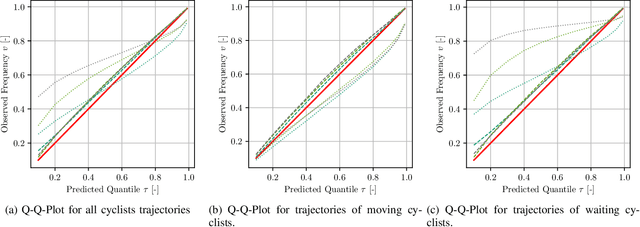
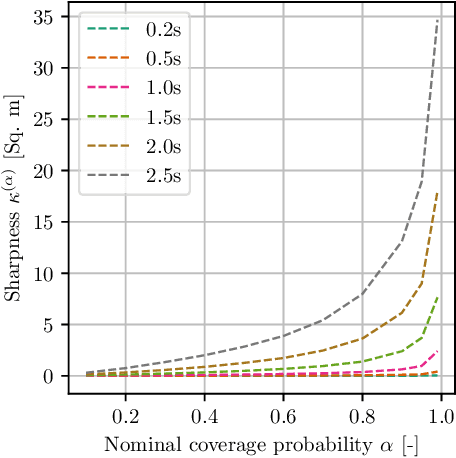
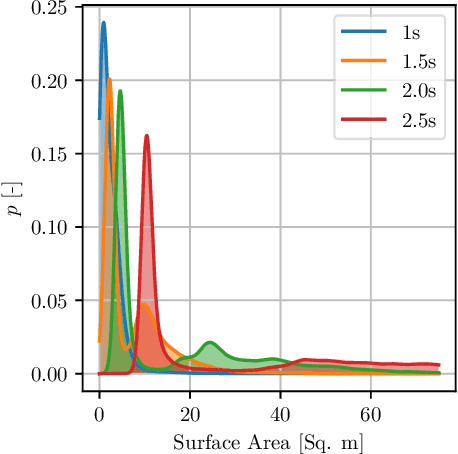
In this article, we present a novel approach to multivariate probabilistic forecasting. Our approach is based on an extension of single-output quantile regression (QR) to multivariate-targets, called quantile surfaces (QS). QS uses a simple yet compelling idea of indexing observations of a probabilistic forecast through direction and vector length to estimate a central tendency. We extend the single-output QR technique to multivariate probabilistic targets. QS efficiently models dependencies in multivariate target variables and represents probability distributions through discrete quantile levels. Therefore, we present a novel two-stage process. In the first stage, we perform a deterministic point forecast (i.e., central tendency estimation). Subsequently, we model the prediction uncertainty using QS involving neural networks called quantile surface regression neural networks (QSNN). Additionally, we introduce new methods for efficient and straightforward evaluation of the reliability and sharpness of the issued probabilistic QS predictions. We complement this by the directional extension of the Continuous Ranked Probability Score (CRPS) score. Finally, we evaluate our novel approach on synthetic data and two currently researched real-world challenges in two different domains: First, probabilistic forecasting for renewable energy power generation, second, short-term cyclists trajectory forecasting for autonomously driving vehicles. Especially for the latter, our empirical results show that even a simple one-layer QSNN outperforms traditional parametric multivariate forecasting techniques, thus improving the state-of-the-art performance.

A Multi-Scheme Ensemble Using Coopetitive Soft-Gating With Application to Power Forecasting for Renewable Energy Generation

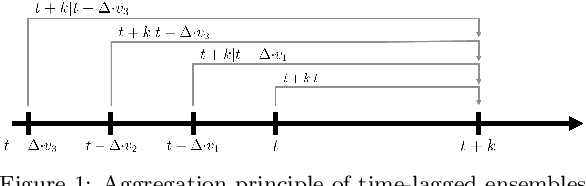
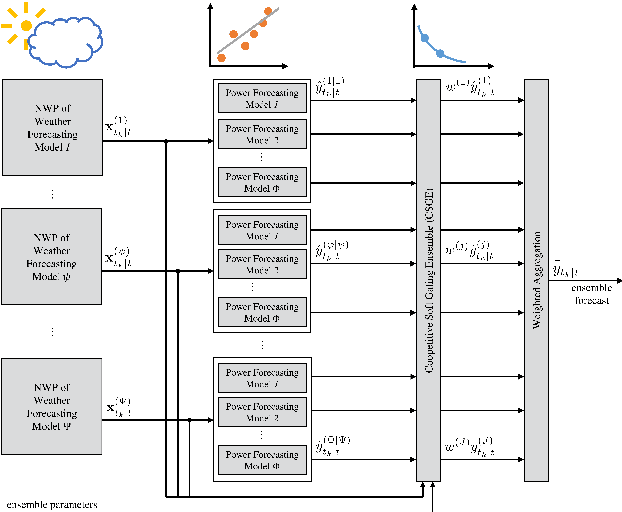
In this article, we propose a novel ensemble technique with a multi-scheme weighting based on a technique called coopetitive soft gating. This technique combines both, ensemble member competition and cooperation, in order to maximize the overall forecasting accuracy of the ensemble. The proposed algorithm combines the ideas of multiple ensemble paradigms (power forecasting model ensemble, weather forecasting model ensemble, and lagged ensemble) in a hierarchical structure. The technique is designed to be used in a flexible manner on single and multiple weather forecasting models, and for a variety of lead times. We compare the technique to other power forecasting models and ensemble techniques with a flexible number of weather forecasting models, which can have the same, or varying forecasting horizons. It is shown that the model is able to outperform those models on a number of publicly available data sets. The article closes with a discussion of properties of the proposed model which are relevant in its application.