ReverseNER: A Self-Generated Example-Driven Framework for Zero-Shot Named Entity Recognition with Large Language Models

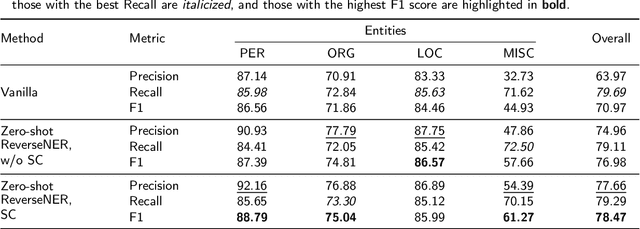
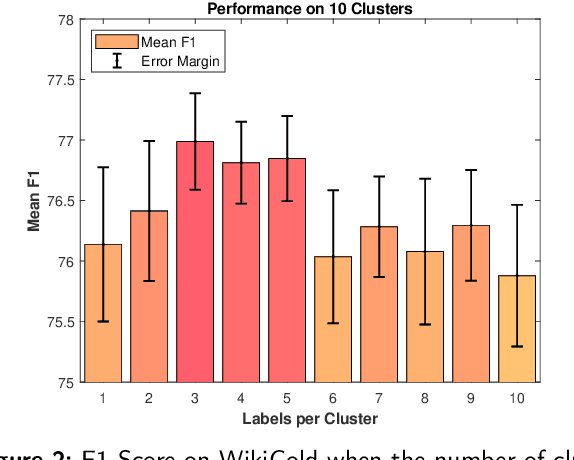
This paper presents ReverseNER, a framework aimed at overcoming the limitations of large language models (LLMs) in zero-shot Named Entity Recognition (NER) tasks, particularly in cases where certain entity types have ambiguous boundaries. ReverseNER tackles this challenge by constructing a reliable example library with the reversed process of NER. Rather than beginning with sentences, this method uses an LLM to generate entities based on their definitions and then expands them into full sentences. During sentence generation, the LLM is guided to replicate the structure of a specific 'feature sentence', extracted from the task sentences by clustering. This results in well-annotated sentences with clearly labeled entities, while preserving semantic and structural similarity to the task sentences. Once the example library is constructed, the method selects the most semantically similar example labels for each task sentence to support the LLM's inference. We also propose an entity-level self-consistency scoring mechanism to improve NER performance with LLMs. Experiments show that ReverseNER significantly outperforms traditional zero-shot NER with LLMs and surpasses several few-shot methods, marking a notable improvement in NER for domains with limited labeled data.

Maximising Quantum-Computing Expressive Power through Randomised Circuits

In the noisy intermediate-scale quantum era, variational quantum algorithms (VQAs) have emerged as a promising avenue to obtain quantum advantage. However, the success of VQAs depends on the expressive power of parameterised quantum circuits, which is constrained by the limited gate number and the presence of barren plateaus. In this work, we propose and numerically demonstrate a novel approach for VQAs, utilizing randomised quantum circuits to generate the variational wavefunction. We parameterize the distribution function of these random circuits using artificial neural networks and optimize it to find the solution. This random-circuit approach presents a trade-off between the expressive power of the variational wavefunction and time cost, in terms of the sampling cost of quantum circuits. Given a fixed gate number, we can systematically increase the expressive power by extending the quantum-computing time. With a sufficiently large permissible time cost, the variational wavefunction can approximate any quantum state with arbitrary accuracy. Furthermore, we establish explicit relationships between expressive power, time cost, and gate number for variational quantum eigensolvers. These results highlight the promising potential of the random-circuit approach in achieving a high expressive power in quantum computing.