Ananda T. Suresh
Data Amplification: A Unified and Competitive Approach to Property Estimation
Mar 29, 2019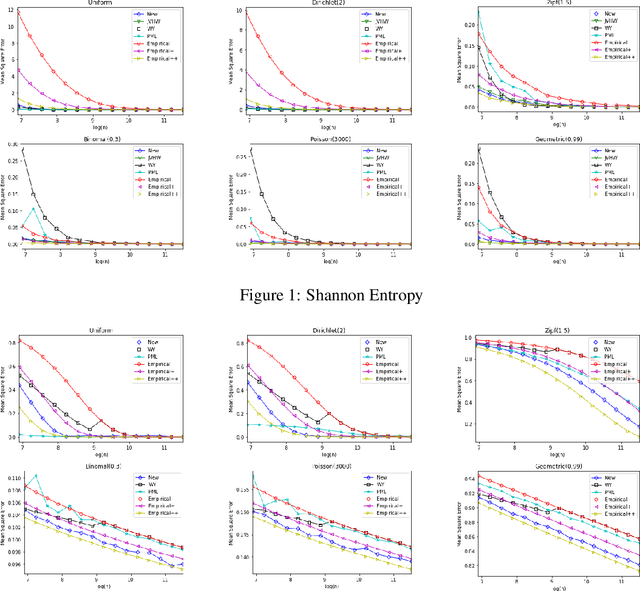
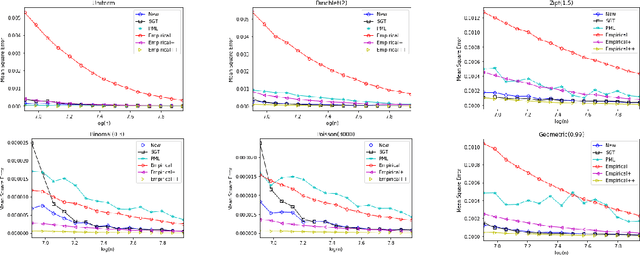
Abstract:Estimating properties of discrete distributions is a fundamental problem in statistical learning. We design the first unified, linear-time, competitive, property estimator that for a wide class of properties and for all underlying distributions uses just $2n$ samples to achieve the performance attained by the empirical estimator with $n\sqrt{\log n}$ samples. This provides off-the-shelf, distribution-independent, "amplification" of the amount of data available relative to common-practice estimators. We illustrate the estimator's practical advantages by comparing it to existing estimators for a wide variety of properties and distributions. In most cases, its performance with $n$ samples is even as good as that of the empirical estimator with $n\log n$ samples, and for essentially all properties, its performance is comparable to that of the best existing estimator designed specifically for that property.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge