Efficient Black-Box Importance Sampling for VaR and CVaR Estimation

This paper considers Importance Sampling (IS) for the estimation of tail risks of a loss defined in terms of a sophisticated object such as a machine learning feature map or a mixed integer linear optimisation formulation. Assuming only black-box access to the loss and the distribution of the underlying random vector, the paper presents an efficient IS algorithm for estimating the Value at Risk and Conditional Value at Risk. The key challenge in any IS procedure, namely, identifying an appropriate change-of-measure, is automated with a self-structuring IS transformation that learns and replicates the concentration properties of the conditional excess from less rare samples. The resulting estimators enjoy asymptotically optimal variance reduction when viewed in the logarithmic scale. Simulation experiments highlight the efficacy and practicality of the proposed scheme

Achieving Efficiency in Black Box Simulation of Distribution Tails with Self-structuring Importance Samplers

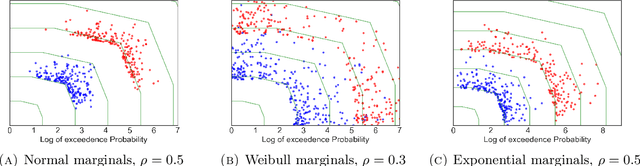
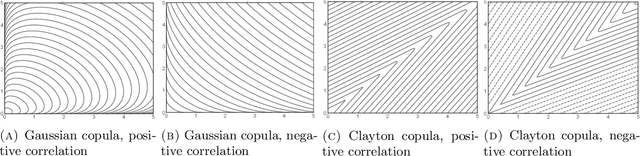
Motivated by the increasing adoption of models which facilitate greater automation in risk management and decision-making, this paper presents a novel Importance Sampling (IS) scheme for measuring distribution tails of objectives modelled with enabling tools such as feature-based decision rules, mixed integer linear programs, deep neural networks, etc. Conventional efficient IS approaches suffer from feasibility and scalability concerns due to the need to intricately tailor the sampler to the underlying probability distribution and the objective. This challenge is overcome in the proposed black-box scheme by automating the selection of an effective IS distribution with a transformation that implicitly learns and replicates the concentration properties observed in less rare samples. This novel approach is guided by a large deviations principle that brings out the phenomenon of self-similarity of optimal IS distributions. The proposed sampler is the first to attain asymptotically optimal variance reduction across a spectrum of multivariate distributions despite being oblivious to the underlying structure. The large deviations principle additionally results in new distribution tail asymptotics capable of yielding operational insights. The applicability is illustrated by considering product distribution networks and portfolio credit risk models informed by neural networks as examples.