Deep Diffusion Models for Seismic Processing

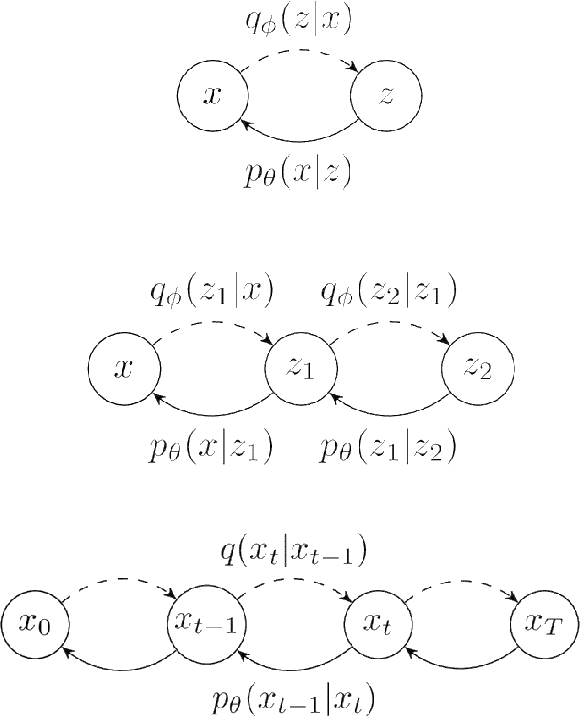
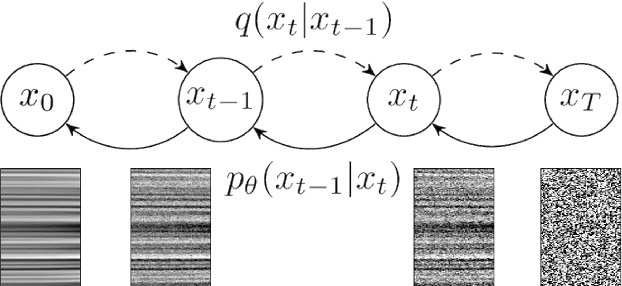
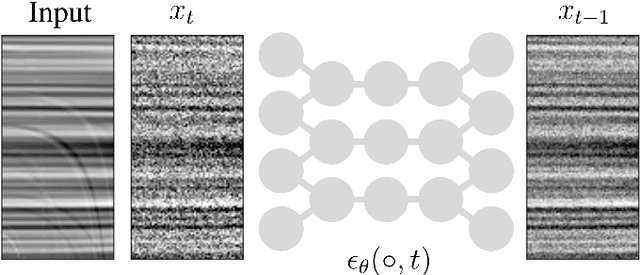
Seismic data processing involves techniques to deal with undesired effects that occur during acquisition and pre-processing. These effects mainly comprise coherent artefacts such as multiples, non-coherent signals such as electrical noise, and loss of signal information at the receivers that leads to incomplete traces. In the past years, there has been a remarkable increase of machine-learning-based solutions that have addressed the aforementioned issues. In particular, deep-learning practitioners have usually relied on heavily fine-tuned, customized discriminative algorithms. Although, these methods can provide solid results, they seem to lack semantic understanding of the provided data. Motivated by this limitation, in this work, we employ a generative solution, as it can explicitly model complex data distributions and hence, yield to a better decision-making process. In particular, we introduce diffusion models for three seismic applications: demultiple, denoising and interpolation. To that end, we run experiments on synthetic and on real data, and we compare the diffusion performance with standardized algorithms. We believe that our pioneer study not only demonstrates the capability of diffusion models, but also opens the door to future research to integrate generative models in seismic workflows.

Dissecting U-net for Seismic Application: An In-Depth Study on Deep Learning Multiple Removal

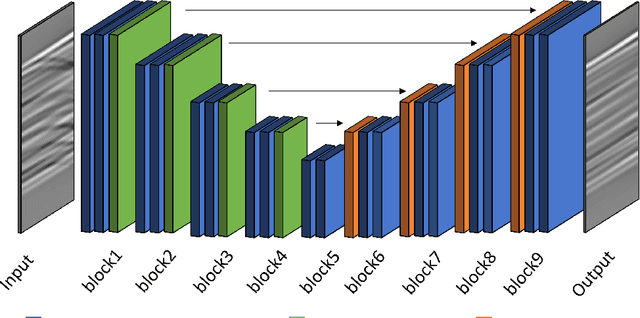
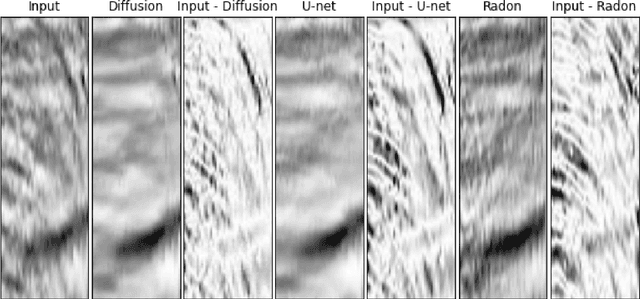
Seismic processing often requires suppressing multiples that appear when collecting data. To tackle these artifacts, practitioners usually rely on Radon transform-based algorithms as post-migration gather conditioning. However, such traditional approaches are both time-consuming and parameter-dependent, making them fairly complex. In this work, we present a deep learning-based alternative that provides competitive results, while reducing its usage's complexity, and hence democratizing its applicability. We observe an excellent performance of our network when inferring complex field data, despite the fact of being solely trained on synthetics. Furthermore, extensive experiments show that our proposal can preserve the inherent characteristics of the data, avoiding undesired over-smoothed results, while removing the multiples. Finally, we conduct an in-depth analysis of the model, where we pinpoint the effects of the main hyperparameters with physical events. To the best of our knowledge, this study pioneers the unboxing of neural networks for the demultiple process, helping the user to gain insights into the inside running of the network.