A Learned Generalized Geodesic Distance Function-Based Approach for Node Feature Augmentation on Graphs

Geodesic distances on manifolds have numerous applications in image processing, computer graphics and computer vision. In this work, we introduce an approach called `LGGD' (Learned Generalized Geodesic Distances). This method involves generating node features by learning a generalized geodesic distance function through a training pipeline that incorporates training data, graph topology and the node content features. The strength of this method lies in the proven robustness of the generalized geodesic distances to noise and outliers. Our contributions encompass improved performance in node classification tasks, competitive results with state-of-the-art methods on real-world graph datasets, the demonstration of the learnability of parameters within the generalized geodesic equation on graph, and dynamic inclusion of new labels.

Learning Label Initialization for Time-Dependent Harmonic Extension

Node classification on graphs can be formulated as the Dirichlet problem on graphs where the signal is given at the labeled nodes, and the harmonic extension is done on the unlabeled nodes. This paper considers a time-dependent version of the Dirichlet problem on graphs and shows how to improve its solution by learning the proper initialization vector on the unlabeled nodes. Further, we show that the improved solution is at par with state-of-the-art methods used for node classification. Finally, we conclude this paper by discussing the importance of parameter t, pros, and future directions.

Variational models for signal processing with Graph Neural Networks

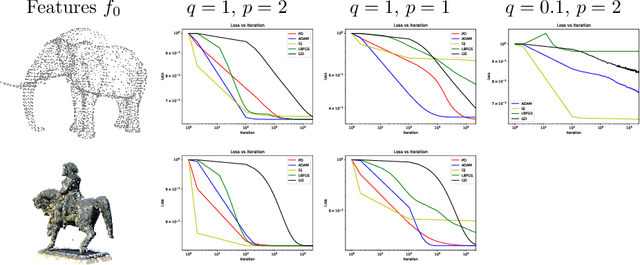
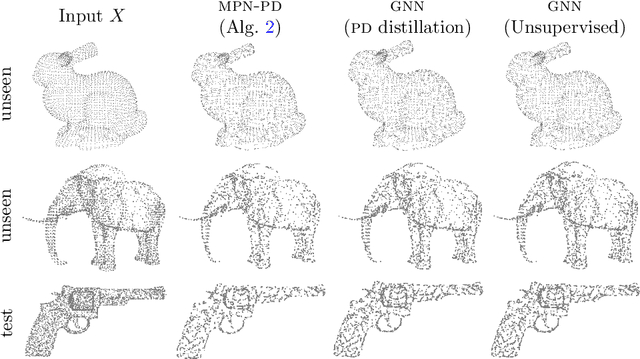
This paper is devoted to signal processing on point-clouds by means of neural networks. Nowadays, state-of-the-art in image processing and computer vision is mostly based on training deep convolutional neural networks on large datasets. While it is also the case for the processing of point-clouds with Graph Neural Networks (GNN), the focus has been largely given to high-level tasks such as classification and segmentation using supervised learning on labeled datasets such as ShapeNet. Yet, such datasets are scarce and time-consuming to build depending on the target application. In this work, we investigate the use of variational models for such GNN to process signals on graphs for unsupervised learning. Our contributions are two-fold. We first show that some existing variational-based algorithms for signals on graphs can be formulated as Message Passing Networks (MPN), a particular instance of GNN, making them computationally efficient in practice when compared to standard gradient-based machine learning algorithms. Secondly, we investigate the unsupervised learning of feed-forward GNN, either by direct optimization of an inverse problem or by model distillation from variational-based MPN. Keywords:Graph Processing. Neural Network. Total Variation. Variational Methods. Message Passing Network. Unsupervised learning