Post-Selection Distributional Model Evaluation

Formal model evaluation methods typically certify that a model satisfies a prescribed target key performance indicator (KPI) level. However, in many applications, the relevant target KPI level may not be known a priori, and the user may instead wish to compare candidate models by analyzing the full trade-offs between performance and reliability achievable at test time by the models. This task, requiring the reliable estimate of the test-time KPI distributions, is made more complicated by the fact that the same data must often be used both to pre-select a subset of candidate models and to estimate their KPI distributions, causing a potential post-selection bias. In this work, we introduce post-selection distributional model evaluation (PS-DME), a general framework for statistically valid distributional model assessment after arbitrary data-dependent model pre-selection. Building on e-values, PS-DME controls post-selection false coverage rate (FCR) for the distributional KPI estimates and is proved to be more sample efficient than a baseline method based on sample splitting. Experiments on synthetic data, text-to-SQL decoding with large language models, and telecom network performance evaluation demonstrate that PS-DME enables reliable comparison of candidate configurations across a range of reliability levels, supporting the statistically reliable exploration of performance--reliability trade-offs.

Optimized Certainty Equivalent Risk-Controlling Prediction Sets

In safety-critical applications such as medical image segmentation, prediction systems must provide reliability guarantees that extend beyond conventional expected loss control. While risk-controlling prediction sets (RCPS) offer probabilistic guarantees on the expected risk, they fail to capture tail behavior and worst-case scenarios that are crucial in high-stakes settings. This paper introduces optimized certainty equivalent RCPS (OCE-RCPS), a novel framework that provides high-probability guarantees on general optimized certainty equivalent (OCE) risk measures, including conditional value-at-risk (CVaR) and entropic risk. OCE-RCPS leverages upper confidence bounds to identify prediction set parameters that satisfy user-specified risk tolerance levels with provable reliability. We establish theoretical guarantees showing that OCE-RCPS satisfies the desired probabilistic constraint for loss functions such as miscoverage and false negative rate. Experiments on image segmentation demonstrate that OCE-RCPS consistently meets target satisfaction rates across various risk measures and reliability configurations, while OCE-CRC fails to provide probabilistic guarantees.

Should I Have Expressed a Different Intent? Counterfactual Generation for LLM-Based Autonomous Control

Large language model (LLM)-powered agents can translate high-level user intents into plans and actions in an environment. Yet after observing an outcome, users may wonder: What if I had phrased my intent differently? We introduce a framework that enables such counterfactual reasoning in agentic LLM-driven control scenarios, while providing formal reliability guarantees. Our approach models the closed-loop interaction between a user, an LLM-based agent, and an environment as a structural causal model (SCM), and leverages test-time scaling to generate multiple candidate counterfactual outcomes via probabilistic abduction. Through an offline calibration phase, the proposed conformal counterfactual generation (CCG) yields sets of counterfactual outcomes that are guaranteed to contain the true counterfactual outcome with high probability. We showcase the performance of CCG on a wireless network control use case, demonstrating significant advantages compared to naive re-execution baselines.

Synthetic Counterfactual Labels for Efficient Conformal Counterfactual Inference

This work addresses the problem of constructing reliable prediction intervals for individual counterfactual outcomes. Existing conformal counterfactual inference (CCI) methods provide marginal coverage guarantees but often produce overly conservative intervals, particularly under treatment imbalance when counterfactual samples are scarce. We introduce synthetic data-powered CCI (SP-CCI), a new framework that augments the calibration set with synthetic counterfactual labels generated by a pre-trained counterfactual model. To ensure validity, SP-CCI incorporates synthetic samples into a conformal calibration procedure based on risk-controlling prediction sets (RCPS) with a debiasing step informed by prediction-powered inference (PPI). We prove that SP-CCI achieves tighter prediction intervals while preserving marginal coverage, with theoretical guarantees under both exact and approximate importance weighting. Empirical results on different datasets confirm that SP-CCI consistently reduces interval width compared to standard CCI across all settings.

Context-Aware Online Conformal Anomaly Detection with Prediction-Powered Data Acquisition

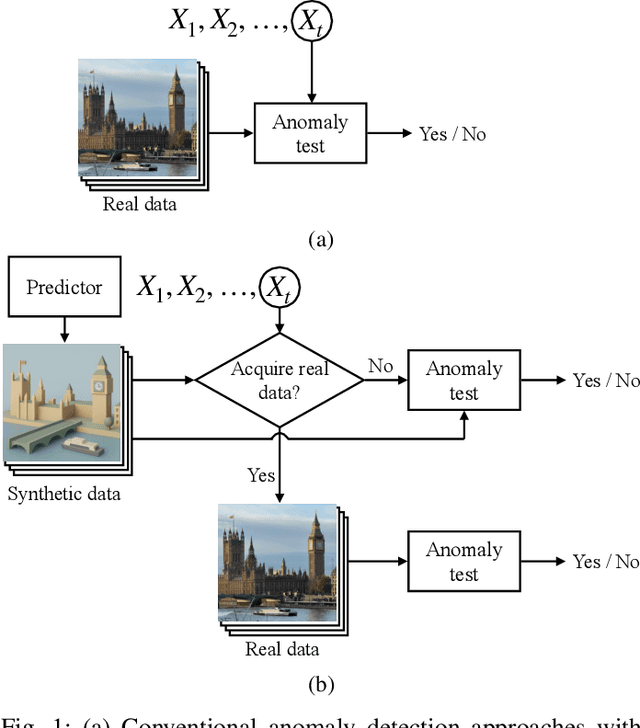
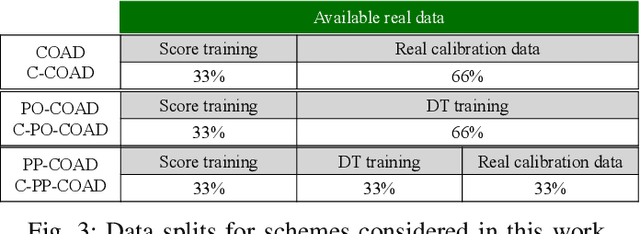
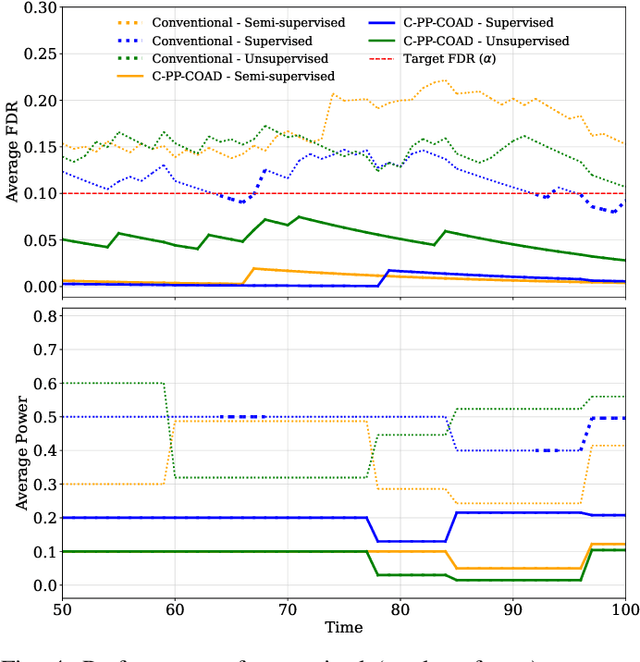
Online anomaly detection is essential in fields such as cybersecurity, healthcare, and industrial monitoring, where promptly identifying deviations from expected behavior can avert critical failures or security breaches. While numerous anomaly scoring methods based on supervised or unsupervised learning have been proposed, current approaches typically rely on a continuous stream of real-world calibration data to provide assumption-free guarantees on the false discovery rate (FDR). To address the inherent challenges posed by limited real calibration data, we introduce context-aware prediction-powered conformal online anomaly detection (C-PP-COAD). Our framework strategically leverages synthetic calibration data to mitigate data scarcity, while adaptively integrating real data based on contextual cues. C-PP-COAD utilizes conformal p-values, active p-value statistics, and online FDR control mechanisms to maintain rigorous and reliable anomaly detection performance over time. Experiments conducted on both synthetic and real-world datasets demonstrate that C-PP-COAD significantly reduces dependency on real calibration data without compromising guaranteed FDR control.

Ensuring Reliability via Hyperparameter Selection: Review and Advances

Hyperparameter selection is a critical step in the deployment of artificial intelligence (AI) models, particularly in the current era of foundational, pre-trained, models. By framing hyperparameter selection as a multiple hypothesis testing problem, recent research has shown that it is possible to provide statistical guarantees on population risk measures attained by the selected hyperparameter. This paper reviews the Learn-Then-Test (LTT) framework, which formalizes this approach, and explores several extensions tailored to engineering-relevant scenarios. These extensions encompass different risk measures and statistical guarantees, multi-objective optimization, the incorporation of prior knowledge and dependency structures into the hyperparameter selection process, as well as adaptivity. The paper also includes illustrative applications for communication systems.

Statistically Valid Information Bottleneck via Multiple Hypothesis Testing

The information bottleneck (IB) problem is a widely studied framework in machine learning for extracting compressed features that are informative for downstream tasks. However, current approaches to solving the IB problem rely on a heuristic tuning of hyperparameters, offering no guarantees that the learned features satisfy information-theoretic constraints. In this work, we introduce a statistically valid solution to this problem, referred to as IB via multiple hypothesis testing (IB-MHT), which ensures that the learned features meet the IB constraints with high probability, regardless of the size of the available dataset. The proposed methodology builds on Pareto testing and learn-then-test (LTT), and it wraps around existing IB solvers to provide statistical guarantees on the IB constraints. We demonstrate the performance of IB-MHT on classical and deterministic IB formulations, validating the effectiveness of IB-MHT in outperforming conventional methods in terms of statistical robustness and reliability.

An Information-Theoretic Analysis of Temporal GNNs

Temporal Graph Neural Networks, a new and trending area of machine learning, suffers from a lack of formal analysis. In this paper, information theory is used as the primary tool to provide a framework for the analysis of temporal GNNs. For this reason, the concept of information bottleneck is used and adjusted to be suitable for a temporal analysis of such networks. To this end, a new definition for Mutual Information Rate is provided, and the potential use of this new metric in the analysis of temporal GNNs is studied.

Quantile Learn-Then-Test: Quantile-Based Risk Control for Hyperparameter Optimization

The increasing adoption of Artificial Intelligence (AI) in engineering problems calls for the development of calibration methods capable of offering robust statistical reliability guarantees. The calibration of black box AI models is carried out via the optimization of hyperparameters dictating architecture, optimization, and/or inference configuration. Prior work has introduced learn-then-test (LTT), a calibration procedure for hyperparameter optimization (HPO) that provides statistical guarantees on average performance measures. Recognizing the importance of controlling risk-aware objectives in engineering contexts, this work introduces a variant of LTT that is designed to provide statistical guarantees on quantiles of a risk measure. We illustrate the practical advantages of this approach by applying the proposed algorithm to a radio access scheduling problem.