Amir Kafshdar Goharshady
Computational Approaches for Stochastic Shortest Path on Succinct MDPs
Jul 17, 2018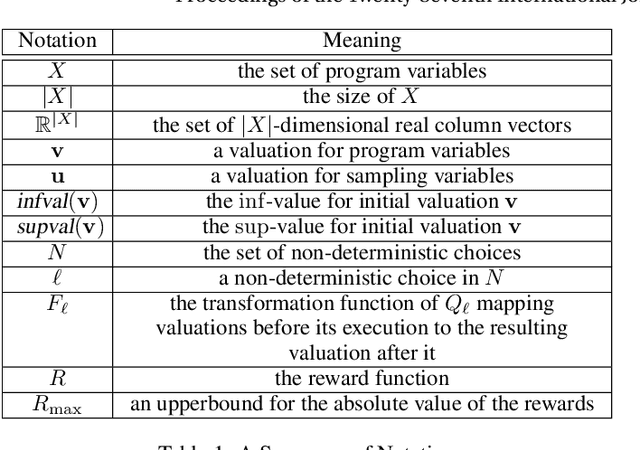
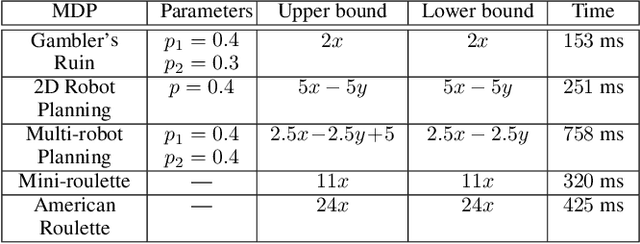
Abstract:We consider the stochastic shortest path (SSP) problem for succinct Markov decision processes (MDPs), where the MDP consists of a set of variables, and a set of nondeterministic rules that update the variables. First, we show that several examples from the AI literature can be modeled as succinct MDPs. Then we present computational approaches for upper and lower bounds for the SSP problem: (a)~for computing upper bounds, our method is polynomial-time in the implicit description of the MDP; (b)~for lower bounds, we present a polynomial-time (in the size of the implicit description) reduction to quadratic programming. Our approach is applicable even to infinite-state MDPs. Finally, we present experimental results to demonstrate the effectiveness of our approach on several classical examples from the AI literature.
A note on belief structures and S-approximation spaces
Jun 02, 2018Abstract:We study relations between evidence theory and S-approximation spaces. Both theories have their roots in the analysis of Dempster's multivalued mappings and lower and upper probabilities and have close relations to rough sets. We show that an S-approximation space, satisfying a monotonicity condition, can induce a natural belief structure which is a fundamental block in evidence theory. We also demonstrate that one can induce a natural belief structure on one set, given a belief structure on another set if those sets are related by a partial monotone S-approximation space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge