A Domain-Theoretic Framework for Robustness Analysis of Neural Networks

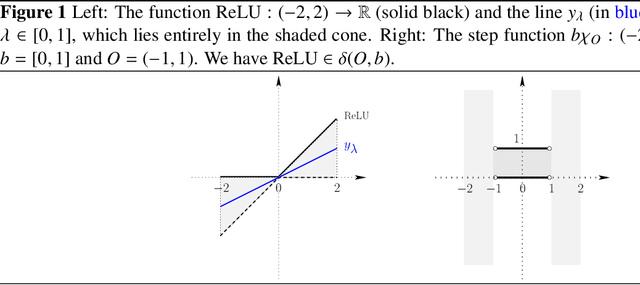
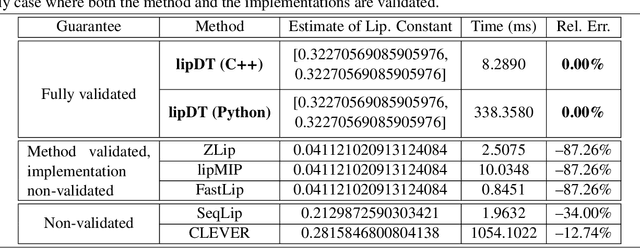
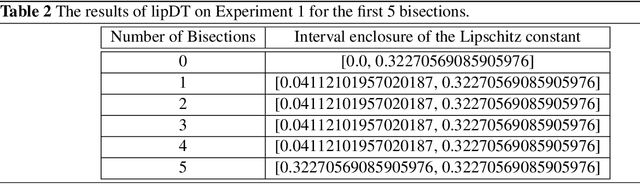
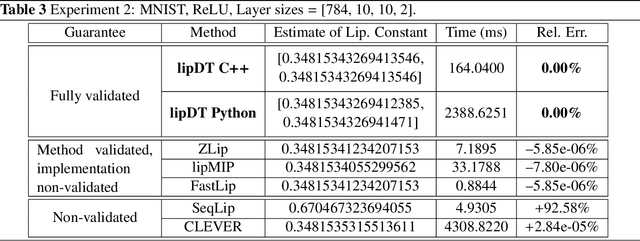
We present a domain-theoretic framework for validated robustness analysis of neural networks. We first analyze the global robustness of a general class of networks. Then, using the fact that, over finite-dimensional Banach spaces, the domain-theoretic L-derivative coincides with Clarke's generalized gradient, we extend our framework for attack-agnostic local robustness analysis. Our framework is ideal for designing algorithms which are correct by construction. We exemplify this claim by developing a validated algorithm for estimation of Lipschitz constant of feedforward regressors. We prove the completeness of the algorithm over differentiable networks, and also over general position ReLU networks. Within our domain model, differentiable and non-differentiable networks can be analyzed uniformly. We implement our algorithm using arbitrary-precision interval arithmetic, and present the results of some experiments. Our implementation is truly validated, as it handles floating-point errors as well.