Amelia Henriksen
Learning to Forecast Dynamical Systems from Streaming Data
Sep 21, 2021
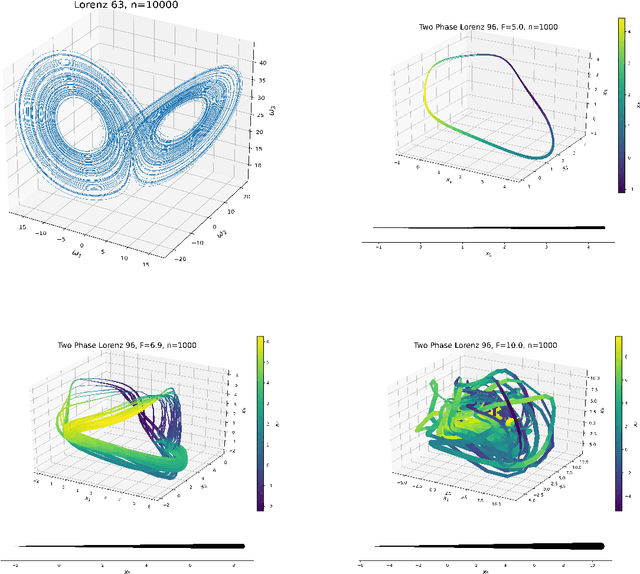
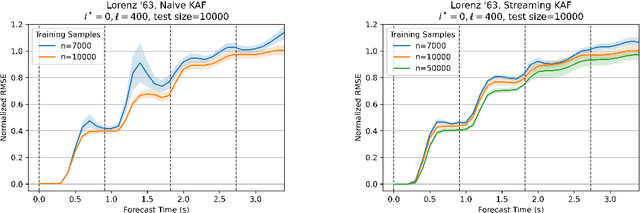

Abstract:Kernel analog forecasting (KAF) is a powerful methodology for data-driven, non-parametric forecasting of dynamically generated time series data. This approach has a rigorous foundation in Koopman operator theory and it produces good forecasts in practice, but it suffers from the heavy computational costs common to kernel methods. This paper proposes a streaming algorithm for KAF that only requires a single pass over the training data. This algorithm dramatically reduces the costs of training and prediction without sacrificing forecasting skill. Computational experiments demonstrate that the streaming KAF method can successfully forecast several classes of dynamical systems (periodic, quasi-periodic, and chaotic) in both data-scarce and data-rich regimes. The overall methodology may have wider interest as a new template for streaming kernel regression.
AdaOja: Adaptive Learning Rates for Streaming PCA
May 28, 2019


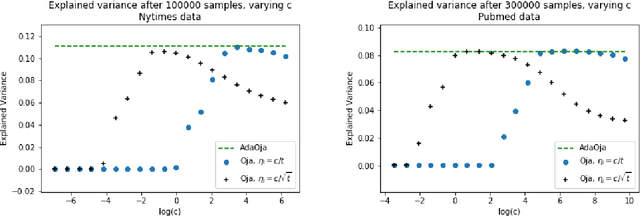
Abstract:Oja's algorithm has been the cornerstone of streaming methods in Principal Component Analysis (PCA) since it was first proposed in 1982. However, Oja's algorithm does not have a standardized choice of learning rate (step size) that both performs well in practice and truly conforms to the online streaming setting. In this paper, we propose a new learning rate scheme for Oja's method called AdaOja. This new algorithm requires only a single pass over the data and does not depend on knowing properties of the data set a priori. AdaOja is a novel variation of the Adagrad algorithm to Oja's algorithm in the single eigenvector case and extended to the multiple eigenvector case. We demonstrate for dense synthetic data, sparse real-world data and dense real-world data that AdaOja outperforms common learning rate choices for Oja's method. We also show that AdaOja performs comparably to state-of-the-art algorithms (History PCA and Streaming Power Method) in the same streaming PCA setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge