Quantum linear algebra is all you need for Transformer architectures

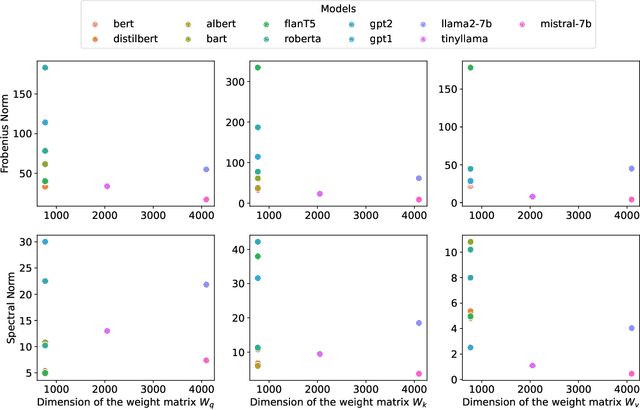
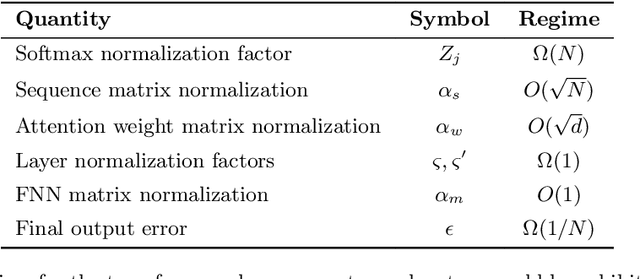
Generative machine learning methods such as large-language models are revolutionizing the creation of text and images. While these models are powerful they also harness a large amount of computational resources. The transformer is a key component in large language models that aims to generate a suitable completion of a given partial sequence. In this work, we investigate transformer architectures under the lens of fault-tolerant quantum computing. The input model is one where pre-trained weight matrices are given as block encodings to construct the query, key, and value matrices for the transformer. As a first step, we show how to prepare a block encoding of the self-attention matrix, with a row-wise application of the softmax function using the Hadamard product. In addition, we combine quantum subroutines to construct important building blocks in the transformer, the residual connection, layer normalization, and the feed-forward neural network. Our subroutines prepare an amplitude encoding of the transformer output, which can be measured to obtain a prediction. We discuss the potential and challenges for obtaining a quantum advantage.

Learning Restricted Boltzmann Machines with greedy quantum search

Restricted Boltzmann Machines (RBMs) are widely used probabilistic undirected graphical models with visible and latent nodes, playing an important role in statistics and machine learning. The task of structure learning for RBMs involves inferring the underlying graph by using samples from the visible nodes. Specifically, learning the two-hop neighbors of each visible node allows for the inference of the graph structure. Prior research has addressed the structure learning problem for specific classes of RBMs, namely ferromagnetic and locally consistent RBMs. In this paper, we extend the scope to the quantum computing domain and propose corresponding quantum algorithms for this problem. Our study demonstrates that the proposed quantum algorithms yield a polynomial speedup compared to the classical algorithms for learning the structure of these two classes of RBMs.