Non-Dominated Sorting Bidirectional Differential Coevolution

Constrained multiobjective optimization problems (CMOPs) are commonly found in real-world applications. CMOP is a complex problem that needs to satisfy a set of equality or inequality constraints. This paper proposes a variant of the bidirectional coevolution algorithm (BiCo) with differential evolution (DE). The novelties in the model include the DE differential mutation and crossover operators as the main search engine and a non-dominated sorting selection scheme. Experimental results on two benchmark test suites and eight real-world CMOPs suggested that the proposed model reached better overall performance than the original model.

An Inverse Modeling Constrained Multi-Objective Evolutionary Algorithm Based on Decomposition

This paper introduces the inverse modeling constrained multi-objective evolutionary algorithm based on decomposition (IM-C-MOEA/D) for addressing constrained real-world optimization problems. Our research builds upon the advancements made in evolutionary computing-based inverse modeling, and it strategically bridges the gaps in applying inverse models based on decomposition to problem domains with constraints. The proposed approach is experimentally evaluated on diverse real-world problems (RWMOP1-35), showing superior performance to state-of-the-art constrained multi-objective evolutionary algorithms (CMOEAs). The experimental results highlight the robustness of the algorithm and its applicability in real-world constrained optimization scenarios.

MOEA/D with Uniformly Randomly Adaptive Weights

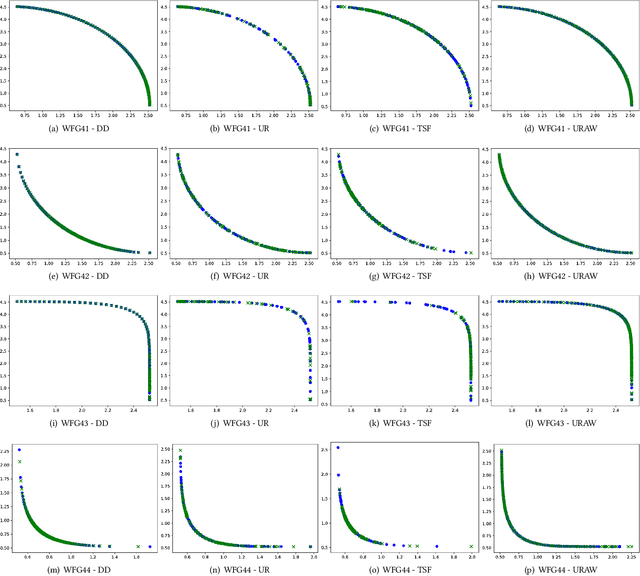
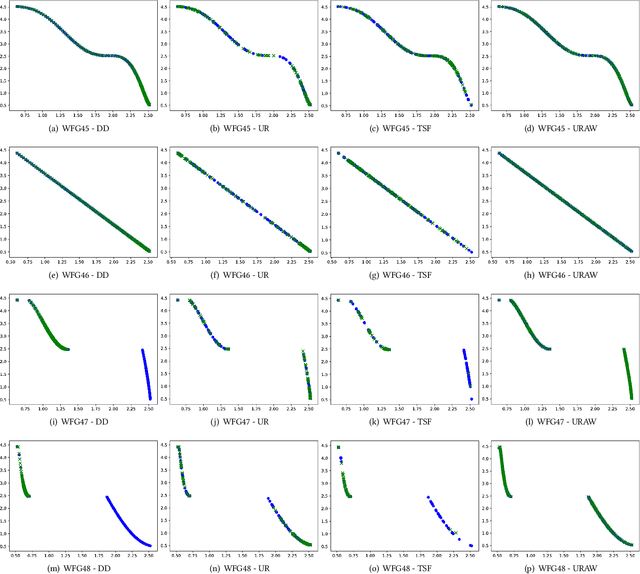
When working with decomposition-based algorithms, an appropriate set of weights might improve quality of the final solution. A set of uniformly distributed weights usually leads to well-distributed solutions on a Pareto front. However, there are two main difficulties with this approach. Firstly, it may fail depending on the problem geometry. Secondly, the population size becomes not flexible as the number of objectives increases. In this paper, we propose the MOEA/D with Uniformly Randomly Adaptive Weights (MOEA/DURAW) which uses the Uniformly Randomly method as an approach to subproblems generation, allowing a flexible population size even when working with many objective problems. During the evolutionary process, MOEA/D-URAW adds and removes subproblems as a function of the sparsity level of the population. Moreover, instead of requiring assumptions about the Pareto front shape, our method adapts its weights to the shape of the problem during the evolutionary process. Experimental results using WFG41-48 problem classes, with different Pareto front shapes, shows that the present method presents better or equal results in 77.5% of the problems evaluated from 2 to 6 objectives when compared with state-of-the-art methods in the literature.