Alok Goswami
Multivariate Dependency Measure based on Copula and Gaussian Kernel
Jan 10, 2018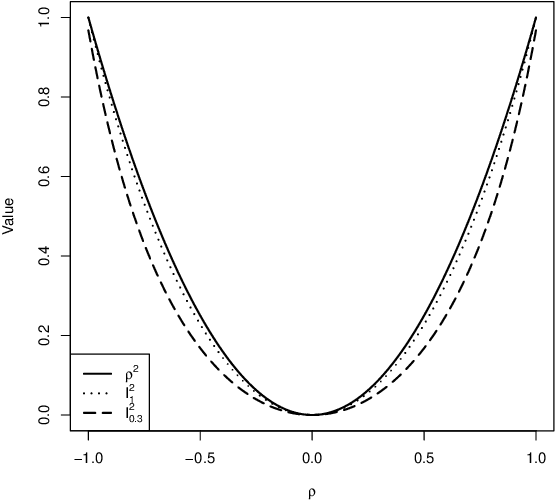
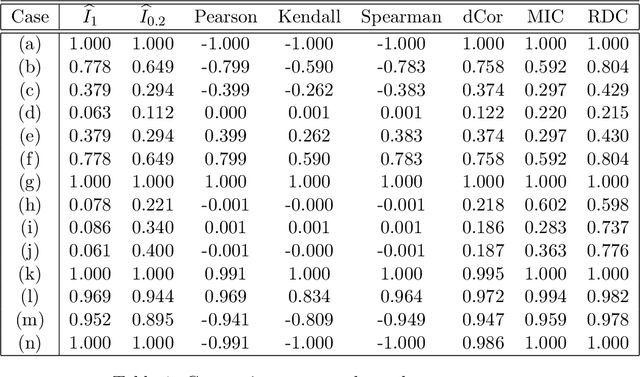
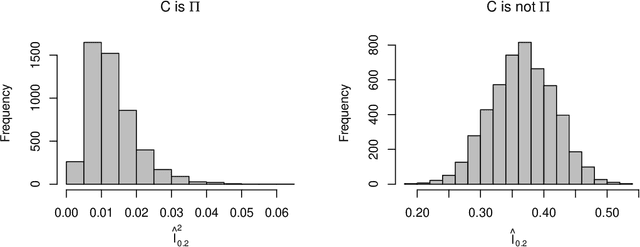
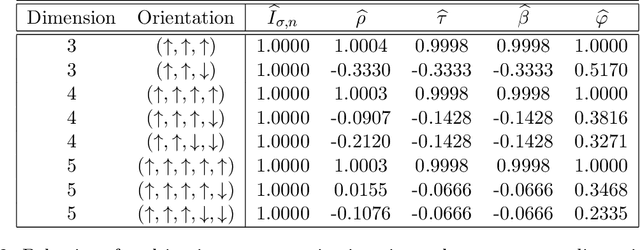
Abstract:We propose a new multivariate dependency measure. It is obtained by considering a Gaussian kernel based distance between the copula transform of the given d-dimensional distribution and the uniform copula and then appropriately normalizing it. The resulting measure is shown to satisfy a number of desirable properties. A nonparametric estimate is proposed for this dependency measure and its properties (finite sample as well as asymptotic) are derived. Some comparative studies of the proposed dependency measure estimate with some widely used dependency measure estimates on artificial datasets are included. A non-parametric test of independence between two or more random variables based on this measure is proposed. A comparison of the proposed test with some existing nonparametric multivariate test for independence is presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge